Crew rescheduling at NS
Every day, Netherlands’ largest railway passenger operator Netherlands railways (NS) faces disruptions due to unforeseen problems with the infrastructure, rolling stock, weather conditions, accidents, etcetera. These disruptions might lead to conflicts in the crew schedules. Human dispatchers try to solve these conflicts by adapting the schedules. However, they have limited solving capacity. During busy days, the workload and pressure on dispatchers is enormous and in extreme cases this could lead to canceled trains or even cancelation of all train traffic. One of NS’ highest priorities is to improve their worst case performance; therefore NS is building on more algorithmic support for human dispatchers. For big disruptions such as blocked tracks, NS has algorithmic support from a solver developed by Potthoff (2010). However, smaller disruptions such as delays, canceled trains and detours are still manually solved by dispatchers. In my thesis the rescheduling for crews in case of small disruptions is modelled as an iterative-deepening depth-first search in a tree, which is combined with several OR techniques obtaining a heuristic method that finds good rescheduling solutions within fraction of seconds. The heuristic focuses on real-life usability and uses the updated rolling stock schedule as input. Some ideas from an actor-agent approach, as discussed in the literature by Abbink et al. (2009, 2010), are combined with other OR techniques.
Methodology
The schedule of a single driver for a day is called a driver’s duty and consists of several tasks that the driver has to perform. An example of a task might be driving an intercity train from station sdep to sarr from time tdep to tarr. There are several rules for duties to be feasible, including labor rules regarding working times and minimum transfer times between consecutive tasks. If these rules are satisfied, we consider duties as feasible. Disruptions lead to infeasibilities in the duties. During small disruptions, dispatchers are usually able to repair infeasible duties into feasible ones by creating unplanned tasks, which are driving tasks that need to be performed by one of the drivers but which are not planned in one of their duties yet. These tasks must be planned into driver’s duties in order to prevent canceled trains. NS also deploys reserve drivers who are standby at railway stations in order to cover tasks in case of disruptions. However, during small disruptions NS prefers not to use reserve duties, they are saved for bigger disruptions which might occur later in time. Planning unplanned tasks in duties is the most time consuming part of the rescheduling process and therefore my thesis focuses on a solution method for unplanned tasks.
When inserting an unplanned task in a duty some new unplanned tasks might be created. These are iteratively solved in order to solve the original unplanned task. Inserting the unplanned task in a duty and iteratively solving new ones can be seen as a search in a tree. To distinguish between different solutions in this tree an objective function is defined. This objective consist of penalties for changed duties, changed breaks and used overtime, in such a way that the chosen solutions are desired by train drivers and dispatchers. Labor rules defined by Dutch regulations for real-time crew rescheduling are satisfied.
The root node of the tree is the original schedule, consisting of all feasible duties and a non-empty set of unplanned tasks M. An edge (s,sii) indicates the insertion of the first unplanned task in M in duty i, where sii denotes the new schedule after insertion. The root node has an outgoing edge to each train driver in the population of train drivers, with exception of the reserve ones. Several OR techniques are combined to find solutions in the tree:
- Insertion of an unplanned task in a duty might not be possible at all. Therefore a basic feasibility check is developed to prune branches of the tree that would lead to impossibilities. The check examines whether the driver is able to take over the unplanned task regarding his route and rolling stock knowledge. Lower bounds on travel time are used.
- After the basic feasibility check the unplanned task can still be inserted in many duties. We define a priority system which predicts how good the task would fit in each of these duties. The system uses prediction values based on linear regression, which are sorted using bucket sort. For example, drivers who are geographically close to the unplanned task or drivers who have lots of spare time in their duty obtain higher priority. The task is inserted in the most promising duty first, expecting to find a solution more quickly.
- A very high prediction value from the priority system indicates that a task is not likely to fit in the duty. If the prediction value is too high, the unpromising part of the tree is pruned. In this way the solving time decreases significantly while hardly any feasible solution is lost.
- Since there are more possible ways to insert a task in a duty we developed a systematic method to insert a task in a duty. The outcome of this method is either: insertion is possible without creating any new unplanned tasks (unconditionally possible), insertion is possible by creating unplanned tasks (conditionally possible), or insertion is impossible.
- If insertion is conditionally possible, we generally branch further using the new unplanned tasks. If lots of unplanned tasks are created, the problem could grow in an unbounded manner. To avoid this, the number of new unplanned tasks created when inserting a task in a duty is maintained below certain threshold. Iteratively the threshold is increased during the execution of the heuristic.
- Solutions in some branches of the tree are of poor quality since they require many changed duties. Therefore, the number of changed duties allowed is bounded. Iteratively this bound is increased. The maximum on this bound is set to 5, since solutions with more changed duties are not desired by NS.
- The objective function is non-decreasing as we search deeper in the tree. Therefore, at each node lower bounds for the solutions are defined. As soon as a solution is found, we set the cost of this solution as upper bound. We fathom parts of the tree with lower bounds higher than the upper bound (fathoming idea from branch and bound). This idea works well when a solution of good quality is found quickly, because large parts of the tree can be pruned.
- Some parts of the tree only have solutions at very (undesired) high costs. Therefore, we prune parts of the tree where the lower bound is above a certain threshold.
- We develop a depth-first iterative-deepening (DFID) search in a tree, in which the depth is bounded by the number of changed duties. DFID combines breadth-first search’s completeness and depth-first search space efficiency, which is optimal when the path cost is a non-decreasing function of the depth of the node (Korf 1985).
Outcomes of time-consuming computations are stored in registers. Whenever such a computation is required again, results from the register are used, saving computation time. The tree search stops as soon as no further explorations occur or two seconds of solving time have elapsed.
Data
The daily schedule of Thursday June 14, 2012 is used as input data. This day was an average work day at NS with over 10,000 tasks planned in about 1,000 feasible duties. There were no unplanned tasks at the beginning of the day. A test instance is created by copying one of the 10,000 tasks and adding the task to the set of tasks. This task is not planned in one of the duties yet and hence is considered as unplanned. We try to solve this unplanned task, meaning that we look for solutions with only feasible duties and no unplanned tasks. This procedure is repeated for each task to create 10,000 test instances. Half of them are used for fine-tuning the heuristic, the other half are used to test the heuristic. For each instance, we assume it is known 45 minutes in advance that the unplanned task is unplanned, meaning that no changes are allowed to any of the duties more than 45 minutes before the start of the unplanned task.
Results
The heuristic is implemented in C++ on an Intel Core i7 processor with 2.96 GB RAM clocked at 2.80 GHz. When searching in the tree, only the changes are saved and not the nodes, since loading the data in the nodes is more time consuming than performing the changes. An overview of the main results include the following items:
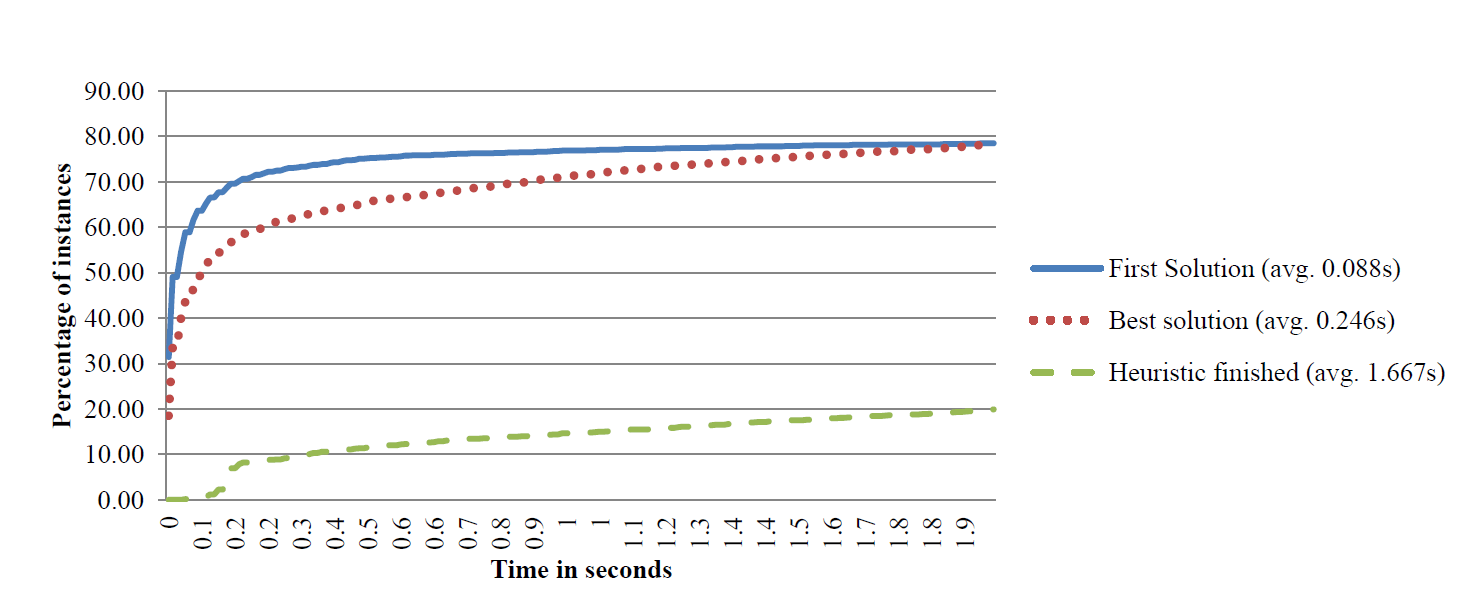
- Consider figure 1, in which the solving time is plotted versus the percentage of instances. Within two seconds, the heuristic finds solutions in over 78% of the instances.
- The average time to find the best solution (that is found within 2 seconds) is only 0.246 seconds, while the first solution was found in on average 0.088 seconds, i.e. good solutions are found quickly.
- The best solution changes on average two duties, uses seven minutes of overtime and changes half a break.
- Consider figure 2, it shows that rescheduling is more difficult around 2 p.m. and during the nights. At NS, many duties start in the early morning and end around 2 p.m., and many new duties start around 2 p.m. Drivers have to return home around 2 p.m. so around this time there are less rescheduling possibilities.
Conclusions and future work
Concluding, the heuristic works fast, delivers good and desirable solutions and outperforms other well-known methods from the literature. My thesis focuses on train drivers only and a similar approach might be developed for train guards. The process from small disruption to unplanned tasks might be modelled. This solution method might be useful to improve the solver for bigger disruptions. It might be interesting to test the solution method in case of bigger disruptions. Last but not least it might be interesting to consider the rolling stock rescheduling and crew rescheduling at once.
References
- Abbink EJW, Mobach DGA, Fioole PJ, Kroon LG, Van der Heijden EHT, Wijngaards NJE (2010) Real-time train driver rescheduling by actor-agent techniques. Public Transp. doi 10.1007/s12469-010-0033-6
- Abbink EJW, Mobach DGA, Fioole PJ, Lentink RM, Kroon LG, Van der Heijden EHT, Wijngaards NJE (2009) Actor-agent application for train driver rescheduling. Proc of Eight Int Conf on Auton Agents and Multiagent Syst, pp 513-520
- Abbink EJW, Mobach DGA, Fioole PJ, Lentink RM, Kroon LG, Van der Heijden EHT, Wijngaards NJE (2009) Train driver rescheduling using task-exchange teams. Proc of the Second Int Workshop on: Optim in Multi-Agent Syst (OPTMAS) at AAMAS 2009
- Korf RE (1985) Depth-first iterative-deepening: An optimal admissible tree search. Artif Intell. doi 10.1.1.91.288
- Potthoff D (2010) Railway Crew Rescheduling: Novel Approaches and Extensions. PhD thesis, Erasmus University Rotterdam
Text by: Thijs Verhaegh