Econometric Roots

Oftentimes, research tends to be an ever-moving train that knows only one direction: forward. Sometimes, however, it is good to look back and see where we have come from. As is often the case with research fields, the exact moment of birth of the field of econometrics is hard to determine. The Norwegian economist Ragnar Frish is generally credited with having founded the discipline of econometrics. However, even though the first known use of the term “Econometrics” dates back to 1910, Frish only published his first important work on econometric methodology in 1929. Other sources, such as Epstein (1983) and Morgan (1990), state that the work of the Cowles Commission in the 1940s is believed to be the starting point of modern econometrics. In this article, we will attempt to offer some perspective on the matter.
Text by: Pepijn Wissing

A statistical basis

A Victorian man by the name of Francis Galton, first cousin of Charles Darwin, first proposed the idea of a regression equation in 1865. Later, Galton studied the way in which intellectual, moral and personality traits tend to run in families. In doing so, Galton notes that, as one generation succeeds another, the outstanding qualities that have characterized the earlier generations tend to fade as generations progress. He describes this phenomenon as tendency to mediocrity; something we now know as central tendency. Galton conducted a detailed statistical investigation of such tendencies; his methodology reached its maturity in 1886 and would later be improved upon by Galton’s disciple Karl Pearson.

The regression model that strongly influenced the early development of econometrics has features that set it apart from the bivariate statistical model used by Galton. The former was the model in which the variable that is plotted on the horizontal axis is subject to experimental manipulation that was extensively used by Ronald Fisher at the Rothamsted Experimental Station. Having been founded in 1843, the Rothamsted Station is one of the oldest agricultural research institutions in the world. When Fisher joined the institution, he was tasked with making sense of the data generated by a series of long-term experiments, measuring the effects of diverse fertilizers on crop yield.

Over the years, Fisher generated many of the statistical methods that are associated with the linear regression model, such as the theory of design of experiments and the theory of hypothesis testing, as well as propounding the method of maximum-likelihood estimation. As such, his first book, Statistical Methods for Research Workers, which was published in 1925, became a standard reference work for scientists in many disciplines, and traces of it are found in the early texts of econometrics.

The experimental regression model of Fisher can be reconciled with the descriptive regression model used by Galton if one rephrases the question to a conditional distribution of the dependent variable y, given the independent variable x. Even though x has its own Gaussian distribution in Galton’s descriptive model, we can still take a specific value of x and ask for the consequent value of y, as illustrated in Figure 1.

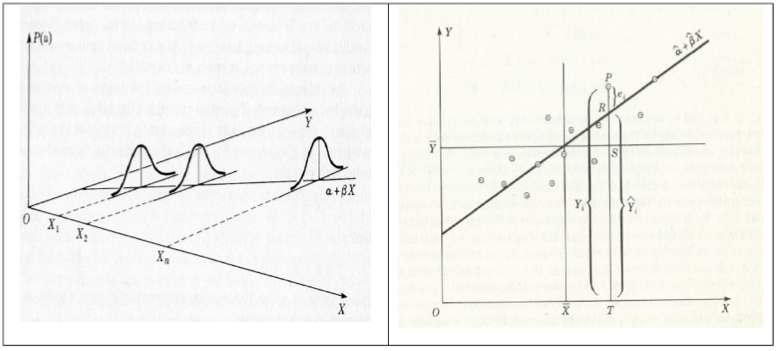
However, we have to be careful with the results obtained from both of these models: there are still some unincorporated bounds on the ranges of the independent variables. For example, using too much fertilizer would scorch the plants and using too much water would also kill them. In econometrics, imposing such bounds is quite uncommon: oftentimes, the main purpose of an estimated model is to form conjectures regarding the effect of values for the independent variable that are impossible (or just very hard) to test for in an experimental set-up. Furthermore, one of the more complex problems in early econometric theory is dealing with the various interdependencies that might exist between the explanatory variables. One of the essential difficulties came to light in the early 1900s, in connection with the statistical estimation of demand curves.

Supply and demand

The estimation of demand curves was one of the major nuts to crack for American researchers throughout the 1920s and the 1930s. The main problem arises from the fact that prices and quantities of economic goods are jointly determined within their markets, by the interaction of supply and demand. In a particularly beautiful anecdote, Alfred Marshall explains why it may be inappropriate to view the matter from one side only. He said:

“We might as reasonably dispute whether it is the upper or the lower blade of a pair of scissors that cuts a piece of paper, as whether value is governed by utility or cost of production. It is true that, when one blade is held still and the cutting is effected by moving the other, we may say with careless brevity that the cutting is done by the second; but the statement is not strictly accurate, and is to be excused only so long as it claims to be merely a popular and not strictly scientific account of what happens”.

 

The implications of the statement above on the statistical determination of demand curves was fully revealed by Elmer Working in 1927; though historical research has shown that others had reached similar conclusions at earlier dates. For example, the Danish economist Jens Warming had reached this conclusion in his commentary on a book published in 1906. Elmer Working began noting that we may describe the prices and quantities that are determined in the market as the jointly dependent variables in the supply and demand equations. A series of diagrams produced by Working to illustrate this idea can still be found in many econometrics textbooks and is shown in Figure 2.

The recognition of the possibility of achieving the identification of the parameters of models with jointly dependent variables motivated a search for efficient methods of simultaneous-equation estimation[1]. This problem was addressed and solved in theory by a group of young statisticians known as the Cowles Commission in the late 1940s and the early 1950s.

The Cowles Commission

The Cowles Commission for Research in Economics was founded in Colorado Springs in 1932 by a businessman and economist by the name of Alfred Cowles. In 1939, the Commission moved to the University of Chicago. In 1943, Jacob Marschak became director of the Cowles Commission. Under Marschak’s directorship, the Commission began an intensive study of the problems of estimation and identification associated with simultaneous equation systems. The inspiration for this line of research had been the work done by Ragnar Frish. In 1948, Tjalling C. Koopmans – yes, this is indeed the man the Koopmans building is named after – became the director of the commission; it was in this period that the definitive work on simultaneous equation estimation was published.

The commission explored three methods: the indirect least-squares method, the method of limited-information maximum likelihood and the method of full-information maximum likelihood. The more considerable achievements of Koopmans and the Cowles Commission were their rigorous development of the theoretical statistical underpinnings of those earlier conceptual ideas and making all of them work together. At the 50th anniversary celebration of the commission, Malinvaud referred to their simultaneous equation methodology as a castle. He said:

“It is a must to go on top of the keep and to look from there at the surrounding landscape. If one does not do so, one will be definitely handicapped and clumsy when making assessments about exogeneity, about identifiability or about estimation bias resulting from interdependence between phenomena.”

However, it is fair to say that the maximum-likelihood methods defeated the practitioners at the time. In the first place, the methods demanded computing facilities that were not widely available. Also, their mathematical derivations were demanding and not widely understood. In the late 1950s and the early 1960s, these methods were effectively reinvented, now by the name of two- and three-stage least squares, in a manner that made them widely intelligible.

Rising opposition to the Cowles Commission by the department of economics at the University of Chicago during the 1950s forced the group to move to Yale University in 1955, where it would be reincarnated as the Cowles Foundation. Electronic copies of the fundamental papers on the subjects mentioned above are available at http:/cowles.econ.yale.edu/, for the interested reader.

An important note on the origin of the fundamental ideas is placed by Morgan (1990). She said: “According to my interpretation of the evidence then, system estimation and structural relations were both well understood (…) before the Cowles work of the 1940s. All that was missing is simultaneity, and it was Haavelmo in 1941, who moved the emphasis away from the individual structural relations (…) towards a model of simultaneous structural relations.” Haavelmo, in turn, owed much of his discussion of structure to Frish’s influence. Frish had, for example, advised that individual equations in macrodynamic systems such as Tinbergen’s should be estimated directly in 1933.

Large-scale macroeconometrics

The work of the Cowles Commission was accompanied by an increasing interest in large-scale macro-econometric models, which were proposed as indispensable aids to governmental decision-making. The Dutch economist Jan Tinbergen developed the first comprehensive national model, which he first built for the Netherlands (in 1937) and later applied to the United States (1939) and to the United Kingdom (1951). For these efforts, Tinbergen received (jointly with Ragnar Frish) the first Nobel prize in economics in 1969.  In the hands of the statisticians of the national central statistical offices (such as the Dutch CBS), these models grew to include hundreds of equations. There were equations for estimating a variety of consumer demands, equations to describe house-building activities in detail, and so forth.

However, the idea of joint or simultaneous determination of certain economic variables met quite some resistance, most notably from Herman Wold. Wold argued that multi-equation econometric models should be structured in a recursive manner, such that preceding equations would predetermine the inputs to each equation. In a paper titled “Causal Ordering and Identification”, Herbert Simon provides an example on the causal relation between (1) poor growing weather, (2) small crop yield and (3) the increasing price of wheat. He establishes a series of equations that determines the  corresponding variables x1, x2 and x3 in sequence, which can be portrayed by writing x1 → x2→ x3. This may be seen as a temporal sequence, although Simon notes that a causal ordering is not necessarily predicated on a temporal ordering.

That said, the existence of a temporal ordering amongst equations can greatly alleviate the problems of identification and estimation, as well as lending a dynamic quality to models. To see this, we consider an elaboration of Simon’s model, in which farmers growing this year’s crops are reacting to last year’s prices. The so-called cobweb model depicts farmers who overreact to these prices, which will cause them to overproduce, which will cause the price to fall. The next year, farmers will again react to prices, now at a lower level. This, in turn, will cause underproduction and a rising price. Whether this repetitive cycle spirals out of control or not, depends on the geometry of the supply and demand curves, as is shown in Figure 3.

Wold did try testing his causal chains against the Cowles simultaneous equations model, with interesting results. See, for example, Wold (1958). In a paper published in 1982, Malinvaud raises the issue briefly, to remark that the simultaneous equations bias has often found to be small enough. However, it has been documented how the large macroeconometric models of the 1950s and 1960s did use Wold’s notions in order to justify the use of the computationally easier OLS technique for estimation. Although Wold may have lost the ideological battle, he did win the practical war.

Dynamic models

In an experimental situation, where one might be investigating the effects of an input variable x on some mechanism, one typically sets the value of x and waits for the system to achieve an equilibrium state, before observing the corresponding value of output variable y. However, in economics, we are often interested in the dynamic response of y to changes in x, given that x might be continuously changing and that the system might never reach an equilibrium state.

In the early days of econometrics, attempts were made to model the dynamic responses primarily by including lagged values of x in the regression equation. The so-called distributed-lag model was commonly adopted. This model typically takes the form of

   

Here, the sequence of coefficients controls the impulse-response function of mapping to and is some error term.

A problem with the distributed-lag formulation is that it is shameless in its use of parameters. Furthermore, since in dynamic econometric context, the sequence  is likely to show strong serial correlation, we may expect the estimates of the parameters to be ill-determined with large standard errors. It is difficult to specify beforehand what form a lag response will take in any particular econometric context. Nevertheless, there is a common presumption amongst economists that the coefficients will all be of the same sign and that, if the sign is positive, their values will rise rapidly to a peak, before declining gently to zero.

Several other models were introduced, such as the model of Koyk (1954), a limiting formulation based on a recursively defined lag-scheme and a second-order recursive formulation. The latter is capable of generating a variety of impulse-responses. However, the failure of its equations to accommodate an adequate range of dynamic behavior may have been one of the main reasons for the demise of the large-scale macroeconometric models.

In reality, much of the practical modeling after the 1950s was on an ad-hoc basis, and it ignored the methodology of the Cowles Commission. The beautiful and grandiose model of the linear simultaneous equation systems was simply not flexible enough for the macroeconometric models, which contained intractable non-linearities in many sectors. To this day, such models have survived, albeit in highly refined forms. However, the prestige has been severely damaged in the 1970s, when it was revealed that their forecasting performance was often far inferior to that of the simple unconditional time-series models of the autoregressive moving average variety.

All in all, I think it is fair to say that no one person can be credited with having founded the discipline of Econometrics. A great deal of people have contributed their ideas and their efforts, and even though these may not have been the ideas that have made the history books, they have still been extremely valuable to the research field by enkindling new ideas in others and revealing potential issues.

 

---

[1] A technique that estimates (a part of) the variables in a system of linear equations, based on the premise that these equations must simultaneously hold.