Sentiment analysis using Support Vector Machines
As long as humans exist, they have been communicating, sharing, searching and storing information. Nowadays, in almost every sector of the economy, data is generated in vast amounts and big data seems to be the magic word as it is considered to be the next big frontier for innovation, competition, and efficiency. Asset | Econometrics already responded to this trend by organizing the Big Data symposium last May.
The biggest challenge of big data is how to extract useful information from it. It is nice to have a large dataset consisting of 350 million rows of customer transaction data related with all kind of other relevant customer characteristics, but if we do not have the tools to process this data and extract useful information from it, this dataset is worthless. This is where the field of machine learning comes into play. Machine learning is a general and popular term for systems that can study and learn from data.
Sentiment analysis
For my master thesis, I applied machine learning techniques in order to construct a sentiment analysis tool for the Greenhouse Group (Eindhoven) as part of an internship. Greenhouse Group is the umbrella organization for six innovative and trend-setting companies in the digital marketing field, i.e., Blue Mango, Fresh Fruit Digital, Blossom, SourceRepublic, FlxOne and WithLocals. Innovation, Dedication and Fun are their core values and are carried out daily by over 150+ dedicated experts. Apart from these six successful companies, the Greenhouse Group also stimulates innovation by organizing a semi-annual Labs program. Greenhouse Group Labs aims to enable students to be the first to work on assignments that revolve around the most innovative technologies and products currently available. This approach helps further fine-tune good ideas while weeding out ideas with less potential. The sentiment analysis tool, for example, is part of the machine learning project. Other projects involved the virtual reality headset Oculus Rift, the EPOC neuroheadset, and next semester there are projects involving the Google Glass and eye tracking technology.
The sentiment analysis tool we developed can be used to quickly determine the sentiment of any message. Therefore, this tool provides several interesting marketing-related purposes. For instance, it is possible to introduce sentiment analytics in customer relationship management systems. The sentiment of incoming mail of customers can be predicted and negative mails can be given a higher priority. More futuristic, and therefore by definition much cooler, sentiment analytics can help in creating automated human conversations between customers and organizations. If a computer is able to determine the sentiment of a user’s message, it can greatly reduce the number of possible replies. It is obvious that these examples would certainly provide any company a big competitive advantage in terms of efficiency and service levels.
Support Vector Machines
By now you may be wondering how machine learning works. In practice, there are a large number of machine learning techniques and algorithms. One of these techniques is the support vector machines technique (SVM). SVM is considered a state-of-the-art machine learning technique and is used in many real-life classification problems. Some of them you are most likely using every day without even realizing. For instance, if you upload a picture on Facebook, nowadays the faces of your friends are automatically tagged. Facebook used SVM in combination with the millions of images we uploaded to make this possible. What I specifically like about this example is that their users actually helped Facebook classify people’s heads in images for free, because initially, they had to manually tag all of their friend’s faces in the images they uploaded. This dataset was then used to create a ‘machine’ that could automatically recognize faces in newly uploaded images.
In short, what a SVM does is finding the best hyperplane that separates the data points of two different classes. For sake of simplicity and because we are creating a sentiment tool, we call these classes ‘positive’ and ‘negative’, and denote them by respectively and . Both sides of the plane represent a different class and this plane can thus be seen as a decision boundary for any new point, because we can easily classify this new point based on which side of the plane it lies. Therefore, after a decision boundary is obtained, a SVM is very useful for making accurate predictions of new data points. Figure 1 presents a simple classification problem and also provides three possible different separating hyperplanes.
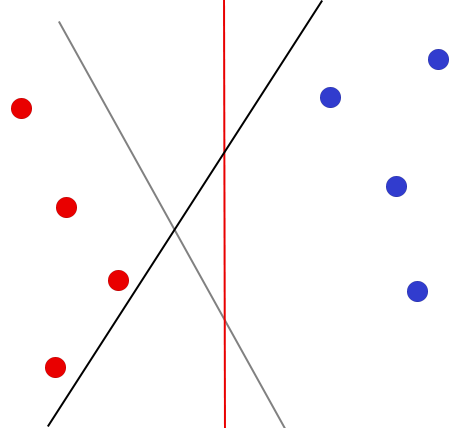
The entire process of constructing a SVM can thus be divided into two parts. In the first part, we train a ‘machine’ by providing it a classified dataset. For the sentiment analysis tool, this data consisted of news articles which were labeled as one of six possible sentiments. Recall that, to keep things simple, we only consider the positive and negative sentiment for this practical report. The training is done by finding the best hyperplane that separates the different classes. This hyperplane is represented by , where represents the dimensionality of the data. Training the machine thus implies finding the best values for and .
In the second part, we are now able to use the trained machine to make predictions about the classification of any data point. For sake of simplicity, we state that positive points lie on the side of the plane for which it holds that and vice versa for negative points. Moreover, we define the variable , which denotes the sentiment classification of message . Using this notation we can state that if data point lies on the correct side of the plane. Note that this can be replaced by , because and can be scaled up such that this equation holds. It is obvious that, once the best hyperplane has been found, it is fairly easy to make predictions, based on which side of the plane the data point is located. The difficult and tricky part is therefore how to find this best separating hyperplane, that is, how to find the values that uniquely determines this hyperplane. For an OR student this is however where things get interesting!
The model
Cortes & Vapnik (1995) tackled this problem by introducing the following (soft-margin) support vector machine optimization problem
The idea behind this model is to find the hyperplane that maximizes the margin around the hyperplane that separates the two different classes (Figure 2). Note that, using basic geometry techniques, it can be shown that denotes the size of this margin. Since we want to maximize this margin, we want to minimize.Obviously, this only works if it is possible to exactly linearly separate the data. Otherwise, there is no margin to maximize and any hyperplane would give a margin of value zero. To solve this issue, Cortes & Vapnik introduced an error-variable . The idea behind this is that we allow data points to violate the margin constraint. This is done by softening the constraint to where .This makes it possible for data points to violate the margin and to even lie on the wrong side of the plane and thus to be misclassified by the hyperplane (Figure 3). However, we do want to penalize data points that violate this constraint. We do this by adding to the objective function, so that we penalize by the proportion of which it violates the constraint. is an additional parameter to set the intensity of the penalty for deviation. Note that if a data point is correctly classified and lies outside the margin, will be equal to zero and thus there is no penalty for that particular data point. Also note that this model is a Quadratic Programming problem, and therefore a QP solver is needed in order to obtain reasonable solutions.


Unfortunately, using a linear classifier is a very restricting method of separating the data and in practice, this method often gives bad results. For instance, Figure 4 gives an example of data that is not easy to separate accurately using a linear decision boundary. Luckily, by applying the so-called `kernel trick’ it is possible to create non-linear classifiers using a SVM. The basic idea behind the kernel trick is to map the original non-linear separable data to a higher dimension in where it can be separated linearly. Figure 5 provides an example of how a simple quadratic function mapping, given by , enables us to map a 1D non-linear separable dataset to a2D dimension where it can be separated linearly. However, it is clear that this mapping results in a significant larger dataset. A polynomial mapping for example would result in going from features to features. Luckily, the kernel trick enables us to create this mapping without visiting this very high dimensional space. The trick is that calculating the inner product of the different messages generates the same meaningful information as mapping all the messages to a very high-dimensional space. So this means we map from features to features, where is the amount of messages. However, this comes at the expense of calculating a lot of inner products which can be quite computational expensive.


Results
Although we are still in the process of obtaining results, preliminary results seem to be promising. For example, for the binary classification case of classifying the sentiment of a message as positive or negative, we are able to obtain an accuracy[1] of around 80%.The major problem we face is how to efficiently solve the SVM model for large datasets. Text mining (extracting information from text) is well known for its large scale. For instance, our dataset of messages contained over 400.000 unique words. Now, representing every message as a vector with the word count of these unique words would imply that every message is represented as a vector of length 400.000, where obviously most of the values are zero. Considering we have around 60.000 classified messages, this would result in a very large QP problem. Also, applying the kernel trick to such a large scale dataset would imply a lot of heavy inner product calculations, which we would like to avoid. Data preprocessing techniques like stemming (reducing every word to its stem) and feature selection methods as Information Gain and Categorical Probability Difference enabled us to reduce this to more usable sizes, varying from 100 to 30.000 by eliminating words that express few sentiment. However, this of course raises new problems. Eliminating too much words that express sentiment results in difficulties predicting the sentiment of a message, whereas removing too few words results in too large data sets and thus results in problems when trying to efficiently train the machine.
As an OR student, however, it is more interesting to improve the SVM training model. The model we discussed in this article is the primal version of the SVM. In practice, however, often the dual version is solved for various reasons. Moreover, we also modeled the problem as a second order cone problem (instead of a QP) and we used the Sequential Minimal Optimization algorithm. Every version has its own pros and cons, but they all have in common that the training time becomes quite long for large data sets. Luckily, we still have plenty of time to develop innovative solutions for all these kind of problems. So, if you are still interested, don’t hesitate to contact us by then!
Footnote
[1] Accuracy was calculated using stratified 10-fold cross-validation.
References
Corinna Cortes and Vladimir Vapnik. Support-vector networks. Machine learning, 20(3):273-297, 1995.
Text by: Thom Hopmans




