Puzzle Nekst 2 2017-2018
The following three puzzles are truly mathematical poetry. For every question the aim is to fill all boxes with the numbers from 1 to 9, each number can only be used once.
The beautiful and elegant result of every number being used exactly once should be enough reward for completing this puzzle! However the board of Asset | Econometrics has offered a crate of beer or a cake for the first respondent to finish the puzzle and send the correct result to nekst@asset-econometrics.nl
There are 24192 possible ways to fill in each of these puzzles. Even if you were able to try one of these combinations every second, it would take you over two weeks to try them all! The logical step therefore is to find some strategies to limit the number of possible combinations.
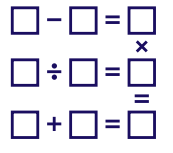
1. Numeric Threesome:

3. Circular sums:
This puzzle is a combination of three puzzles, try to fill the boxes in the following puzzle with the numbers from 1 to 9, using every number only once. The result should be that in every circle the sum of all the numbers is equal to 11. When you have finished this puzzle, try again for the subsequent sums of 13 and 14.

Answer of Puzzle NEKST 2 2017-2018
Written by Bernard van den Broek
The basis of the puzzle of Nekst 2 is easy to explain: 3 puzzles, 9 boxes per puzzle and the numbers 1 to 9. Every puzzle has its own rules. The basic mathematical rules like multiplication and summation are the most important tools to solve the puzzles. Next to that, you still need trial and error and logical sense.
1. Numeric Threesome:
The first puzzle was the numeric threesome. I directly noticed that the number 1 could not fit in the second row or in the last column. Dividing by 1 or multiplying by 1 will always give you the same number as already stated before and that was not allowed. I also noticed that the numbers 2, 4 and 8 should be stated in the second row or last column because there are no other ways to create these equations. The numbers 2, 4 and 8 cannot be the answer on the division calculation. Assume that the answer is 4: 4 times 3 is greater than 9 (we cannot use 1 here and 2 has already been used), so 4 is no option. Assume that the answer on the division equation is 2. Unfortunately, we can easily see that the number 6 should be used twice which is not possible. As a result, the numbers 2, 4 and 8 should be in the last column. To make the division fitting we place the 2 in the middle of the column so we can create the calculation 6 divided by 3 is 2. The number 9 should be in the left upper corner. There is no other place to fit this number. That is why the equation 9 – 5 = 4 is made. The last equation is simply: 1 + 7 = 8. Maybe you think this is a very long explanation for the simplest puzzle, but as a result, there is at least one puzzle I explained well.
2. Unequal equations
The second puzzle was hard to solve because of the important role of trial and error instead of logical sense. I will not bother you with the trial and error part, because that would be very boring to read. The logical part is about noticing where some numbers can and cannot be placed. Just like in the first puzzle, the number 1 cannot be located everywhere. To keep it simple we can say that the number 1 cannot be stated in the third box of the first row and in the first two boxes of the second row. I also noticed that the number 5 is a number with a special property. If you multiply 5 with an arbitrary number, the solution always ends with a 0 or a 5. It is not allowed to place a number twice, therefore 5 cannot fit the second, third and last box of the first row and not in the first, second and last box of the second row. I found one last property before my endless trial and error process started. The first box of the row consists a number lower than 5. An integer higher than 1, multiplied by a number more than 50, will result in a number higher than 100, which is not possible. After this conclusion, the trial and error began and never stopped. Unfortunately I made a calculation error which hold me back from obtaining the right answer immediately. The lack of my handwriting skills could have caused this as well. After hours of puzzling during a long ride from Ede to Tilburg, I arrived in Tilburg and went to my lecture. During this lecture, which was a little boring, I saw the solution: 27 * 3 = 81 and 6 * 9 = 54.
3. Circular sums
The last puzzle contains 5 circles. The two outmost circles contain 2 boxes per circle, the other 3 circles hold 3 boxes per circle. There are 9 boxes in total, so there are 4 boxes which are located in 2 different circles. The sum of all numbers in a circle should be 11 (and later on 13 and 14). This already gave me some clue towards the solution. If the sum of each circle is 11 and there are 5 circles, the total sum of all circles should be 55. The sum of all numbers 1 to 9 is 45. As a result, the overlapping boxes (located in 2 different circles) should have a sum of 10. The 4 unique different nonnegative numbers which have a sum of 10 are 1, 2, 3 and 4. This was my starting point. The number 9 could not be in the middle because the sum would be greater than 11. So, 9 should be in the first or in the last box. The following number is 2 in order to make the sum equal to 11. At the other side of the circle, there should be the number 8 and as a result the number 3. Other numbers will not fit. Again this puzzle has a little part of trial and error. Thinking logically will give you the following order: 925461738 or 837164529, both correct answers to the puzzle.
The other two puzzles (sum of all numbers 13 and 14) are a little harder, because they do not have a starting point like the sum of 11 had. The 4 overlapping boxes now have a sum of 20 and 25 respectively, leading to a lot of possible combinations of 4 digits. Therefore the trial and error part (probably you began to hate these words) was very useful. An helpful trick is the combination of 13 and 14. The number of different combinations of 2 integers is less than with the sum of 11. As a result, this part becomes easier. Concluding Bernard’s long story: the solutions are 765283194 and 592347168 (and vice versa) for 13 and 14 respectively.
As you might have noticed, some of the puzzles do not have a clear explanation. I hope you tried to solve the puzzles and found the solution by yourself (most of you are econometricians so you might be good with numbers). If not or if you still have a question about the explanation, feel free to contact me.