Puzzle Nekst 3 2014-2015
Now that spring is in the air, it is time to break our head over something more cheerful than Stieltjes integration or identically independent distribution samples. For this puzzle, we are going to have a look at an acrobat with a fairly strange act. However, we would like to state that no participants should try to perform this act at home themselves.
Our acrobat is performing an act in which he walks over a rope. He starts at the left end and starts walking to the right, only taking one step at a time, which equals a distance of ten centimeters. After each step his companions stretch the robe by one meter to make the act more interesting.
Hence the act is as follows: start at the left, step, stretch, step, stretch, etc. Every combination of a step plus a stretch takes exactly fifteen seconds. Will the acrobat ever reach the end of the robe and hence finish his act? If so, how long will it take him?
Please send your solution to Nekst@Asset-Econometrics.nl before the 20th of May. A crate of beer or a delicious pie, whichever the winner prefers, will be waiting for whoever has the best (partial) solution. Please note that, as before, every recipient of this magazine is eligible to send in their solution, so members of the department are invited to participate as well. Good luck!
Dennis Jaheruddin is the winner of the previous puzzle. As a reward, he can come and pick up a crate of beer or a pie at room E1.10. The solution of the previous puzzle was 1/2.
Explanation Puzzle Nekst 2 2014-2015
The puzzel from Nekst 2 (2014-2015) concerned a network of bridges from Tilburg-North to Tilburg-South (Figure 1) for which we would like to find the probability that student Henk will be able to cross the water, given the fact that every single bridge has a probability of ½ to collapse. As usual, there are multiple manners to solve such a problem. For instance, it is possible to view the problem as a search for the cheapest route, after which Dijkstra’s algorithm can be used to find one, for example with the help of Matlab. However, a different and more direct approach can be used as well, namely by using the property of symmetry.
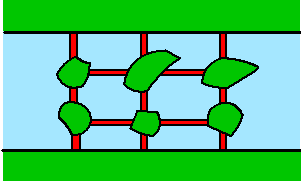
In order to do this, we add six (blue) lakes and six (yellow) sailing routes in our original Figure 1. With this new visualization (shown in Figure 2) it becomes clear that the probability of P[Henk can not cross the water] is equal to the probability of P[Henk can sail from East to West], as in fact these two different networks are identical. If a bridge collapses, it will supply (part of) a sailing route, but not a walking route, and a still existing bridge on the other hand results in (part of) a walking route, but not in a sailing route.
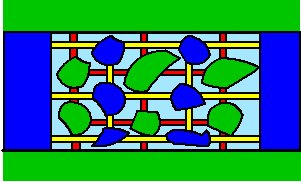
Now as both probabilities are equal AND complementary, we can deduce that their probabilities must be 1/2.




