A mathematical illusion called democracy
The Dutch state representative elections and, even more important, the presidential elections of the USA between Barack Obama and Mitt Romney are just behind us. Of course, you expect these Western elections to be fair and democratic. However, this might not always be the case, as was shown by Nobel Prize winner Kenneth Arrow.
Impossibility Theorem
Elections can be regarded as democracy in action. Citizens go to polls and express their preferences and somehow all these preferences should be aggregated in order to make a joint decision. Consider the following example. In 2000, George W. Bush won the presidential elections with half a million votes less than his opponent Al Gore. This outcome can be explained by means of the district system that is being applied in the USA. This system comes down to a country being split up in different constituencies. The winner of every district will send his state representatives to the parliament, depending on the amount of inhabitants the district has. This system sometimes causes paradoxes as explained in the previous example. On the contrary, in the Netherlands the proportional representation system is being applied. This means that when a political party receives for example 27% of the votes, this party will also gain 27% of the seats in the parliament. Looking back at the elections between Bush and Gore, a proportional representation system would have resulted in a different outcome. Therefore, the choice of which voting method to apply is of crucial importance.
Now you can ask yourself the following question: does there exist an ideal voting method? According to Kenneth Arrow, the answer is ‘no’ – if by ‘ideal’ we are talking about a preferential voting method that satisfies certain criteria that a reasonable and democratic voting method should have. In other words, there is not a single electoral system with all the properties you would expect a fair electoral system to have. For this mathematical result, Arrow received the Nobel Prize in Economics in 1972. Arrow was concerned with arriving at an aggregate social ranking R defined over the set of potentially available social states A, B, etc. The basis of the social ranking R is taken to be the collection of individual rankings {Ri}, with any Ri standing for person i’s preference ranking over the alternative social states open for social choice. It is this functional relation that Arrow calls the ‘social welfare function’. In other words, voters rank all candidates in order of preference and based on these rankings, the method produces an outcome, which is another ranked list of all candidates that is supposed to represent the joint will of the people.
Arrow’s Axioms
Kenneth Arrow set up a few axioms that a democratic system should have. Of course, Arrow’s theorem is often being investigated and for that reason there are different ways to formulate his work. One way to formulate his theorem is by using the following axioms.
• Universality: Each individual voter ranks the n candidates from 1 to n. The candidate ranked i is preferred to all other candidates ranked j where j > i. There are no further restrictions on which rankings are allowed.
• Transitivity: The societal outcome of an election procedure is a ranking with some boundaries. If the society prefers candidate A to candidate B and prefers candidate B to candidate C, then A is ranked above B and B is ranked above C. Because A is ranked above C, the society prefers A to C, too.
• Unanimity: If all voters prefer candidate A to candidate B, then the societal ranking should also place A above B.
• Independence of Irrelevant Alternatives: The societal ranking of a pair of candidates A and B should only depend on how the voters rank these two candidates. To rank these candidates, it is irrelevant to incorporate how the voters rank other candidates. More specifically, suppose that the society ranks A above B and C. If some voters suddenly decide to change their ranking of B and C, then it should not affect the societal ranking of A and B. In other words, A should still be ranked above B.
Taken individually, these axioms appear to place logical requirements upon an election procedure. However, to Arrow’s surprise, the only election procedure that satisfies the above requirements is not much of an election procedure at all. For three or more candidates, the only procedure that satisfies the above four requirements is a … dictatorship. In such a system, the outcome of an election always agrees with a specified voter’s preference. This voter is referred to as the ‘dictator’. With Arrow’s democratic commitment, he added a fifth axiom.
• Non-dictatorship: There is no person i such that whenever this person prefers A to B, then socially A is preferred to B, no matter what others prefer.
A ‘Brief’ Proof
The proof of the Arrow theorem presented here follows Arrow’s own line of reasoning, but through some emendations that make it rather easy to follow. Let A = {A, B, …, C} be a finite set of at least three possible alternatives. A transitive preference over A is a ranking of the alternatives in A from top to bottom, with ties allowed. Let us consider a society with N individuals, each of whom has a (potentially different) transitive preference. An electoral constitution is a function which associates with every N-tuple of transitive preferences an aggregated transitive preference called the social preference. Let us first add an extreme lemma. Let alternative b be chosen arbitrarily. At any profile in which every voter puts alternative b at the very top or very bottom of his ranking of alternatives, society must as well (even if half the voters put b at the top and the other half put b at the bottom). Now suppose to the contrary that for such a profile and for distinct a, b and c the social preference puts a ≥ b and b ≥ c. By the axiom of independence of irrelevant alternatives, this would continue to hold even if every individual moved c above a, because that could be arranged without disturbing any ab or cb votes (for b occupies an extreme position in each individual’s ranking). By transitivity, the social ranking would then continue to put a ≥ c. However, by unanimity it would also put c > a, which is a contradiction proving the lemma.
Next we argue that there is a voter n* = n(b) who can move b from the very bottom of the societal ranking to the very top by his vote. To see this, let each voter put b at the very bottom of his ranking of alternatives. By unanimity, society must as well. Now let the individuals from voter 1 to N successively move b from the bottom of their ranking to the very top, leaving the other relative rankings unchanged. Let n* be the first voter whose change causes the social ranking of b to change. Denote by profile I the list of all voters rankings just before n* moves b, and denote by profile II the list of all voter rankings just after n* moves b to the top. Since in profile II b has moved off the bottom of the societal ranking, we deduce from our first argument that the social preference corresponding to profile II must put b at the very top. Now we argue that n* = n(b) is a dictator over any pair ac not involving b. Choose one element, say a, from the pair ac. Construct profile III from profile II by letting n* move a above b, so that a >n* b >n* c, and by letting all the agents n ≠ n* arbitrarily rearrange their relative rankings of a and c while leaving b in its extreme position. By independence of irrelevant alternatives, the social preferences corresponding to profile III would necessarily put a > b (since all individual ab votes are as in profile I where n* put b at the bottom), and b > c (since all individual bc votes are as in profile II where n* put b at the top). By transitivity, society must put a > c. By independence of irrelevant alternatives, the social preference over ac must agree with n* whenever a >n* c.
We conclude by arguing that n* is also a dictator over every pair ab. Take a third distinct alternative c to put at the bottom in the construction as before. There must be a voter n(c) who is an ab dictator for any pair ab or ba, not involving c. But agent n* can affect society’s ab ranking, namely at profiles I and II, hence this ab dictator n(c) must actually be n*. Now we have proven that the only electoral system which meets the first four axioms must be a dictatorship. When adding the fifth axiom, non-dictatorship, one can see that there is not a single electoral system which serves all the five axioms.
From Impossibilities to Possibilities
Often, the result of Arrow’s theorem is misunderstood. It does not mean that a democratic constitution is doomed to failure and that only dictators are sound political institutions. If the used axioms are an ideal that cannot be met, then other, less stringent, criteria should be used to compare and evaluate election procedures. For that reason, the selection of the ‘best’ electoral system is a decision about which of the mentioned axioms is less important to the application at hand. In 1785, Nicolas de Condorcet considered what would happen on elections between all pairs of candidates and generalized the majority rule in a different manner. Consider the following example in which five voters rank the four candidates A, B, C and D.
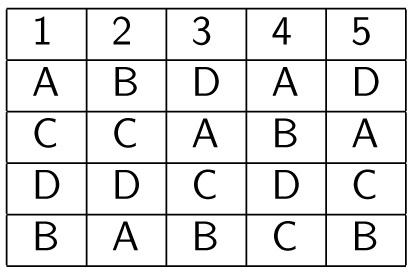
When just considering the first preferences, candidate A would win. Condorcet argued that a candidate that defeats each other candidate in head-to-head elections under the majority rule should be elected, which is called the ‘Condorcet winner’. For example, D defeats A, because three voters prefer D to A (columns 2,3 and 4) while only two voters prefer A to D (columns 1 and 5). Similar calculations can be used to show that D defeats A, B and C in pairwise contests. This is a different outcome compared to the outcome received from just considering the first preferences.
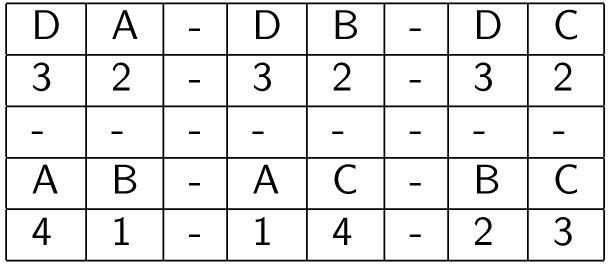
So what is more fair? Pairwise comparison contains more information than when only regarding the first preferences. Therefore, this method can be considered as more reliable and fair, since you not only know which party is preferred the most, but also which party is disliked the most. A disadvantage of this method compared to the majority principle is the fact that it is more difficult to carry out in real life.
Theoretically, there are numerous electoral system to come up with. However, as Kenneth Arrow proved, there is not a single system which meets all the requirements you would expect a democratic system to have. A best procedure may depend on context and which properties are deemed important for the election. One thing we can say for sure: do not vote on which election procedure to use!
Tekst by: Suzanne Vissers
References
(1) Geanakoplos, J. (2005). Three Brief Proofs of Arrow’s Impossibility Theorem. Economic Theory, 26, p. 211-215.
(2) Jones, M.A. Mathematics and Voting: More Than Just Counting Votes. Retrieved from http://www.whydomath.org/node/voting.index.html.
(3) Collins, N. (February 8, 2003). Arrow’s Theorem Proves No Voting System is Perfect. The Tech, 123 (8). Retrieved from http://tech.mit.edu/V123/N8/8voting.8n.html




