Bloodthirsty Queens and Wandering Knights
The game of Chess is hundreds of years old and is widely considered to be the pinnacle of strategic games. Although the basic concept seems rather simple at first, everyone who unsuspectingly played their first match and was forced to surrender only a few moments later will know that there is definitely a lot more to it than meets the eye. To deal with the sheer complexity of the game, we could call in the help of – you guessed it – mathematics.
First and foremost, you might be wondering why we are at all able to link mathematics and chess. This is possible because both concepts are based on logic. Any mathematical reasoning and any chess reasoning (at least, any brute-force, tactical reasoning and to some extent the more abstract concepts and strategies) can be reduced to more basic, formalized logic systems, which is what enables us to have calculators and chess computers. Every element of the chess game is well-defined, which makes it theoretically possible to fully grasp it though logic and mathematics. However, the complexity of the game gives rise to less well-defined themes and concepts, which are far easier for the mind to grasp than brute-force tactics, which even computers cannot solve completely.
Aside from the typical game of chess, many more intriguing problems have been constructed using just the chessboard and its pieces. These problems by themselves are usually not too relevant for the game itself. For example, having eight queens on the board that would legally be able to capture each other is simply impossible with only two players. However, these problems do illustrate quite nicely how mathematics might be applied to break down chess.
The n queens problem
The first problem we will discuss is the so-called n queens problem, which is formally defined as the problem of placing n queens on an n-by-n chessboard in such a way that no two queens are able to capture each other in a single move. Since a normal chessboard is 8-by-8 squares large, this problem is usually referred to as the eight queens problem, but the same principle holds for any n.
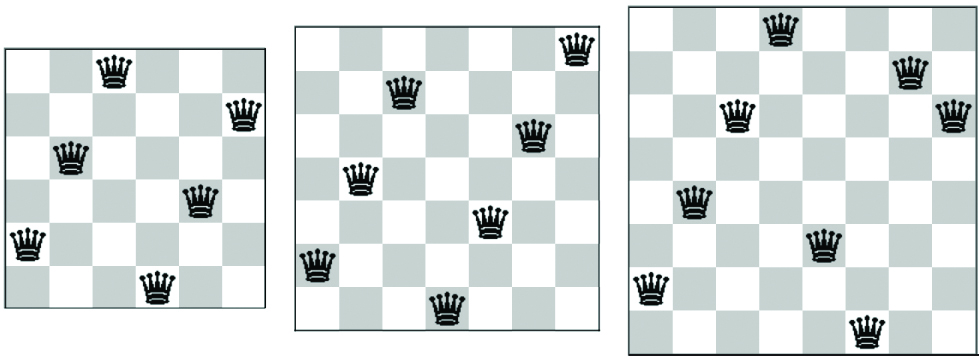
For the sake of simplicity, we will first consider a 4-by-4 board. A solution to the four queens problem is shown in Figure 1. As a matter of fact, there is only one fundamental solution to four queens, since every other solution is the result of some symmetry operation (rotation or reflection) from this one. For a board of this size, a solution can relatively easily be found by simply trying a few positions. However, as you might imagine, the larger you choose your n, the harder it becomes to ‘just see’ a solution: if we increase the board size to 8-by-8, the problem already has 92 distinct solutions that can be reduced down to twelve fundamental solutions.

However, the difficulty of the problem does not lie in the finding of a single explicit solution. If the goal is to find a single solution, the search requires no combinatorics whatsoever. In Figure 2, you might notice that for n=6, 7 and 8, the shown solutions exhibit a stair-stepped pattern. For every n ≥ 4, a solution with a similar pattern exists, and can be obtained using the heuristic below.
Construct a list containing all numbers 1, 2 , … , n in the following manner:
- If the remainder from dividing n by 6 is not 2 or 3, then the list is simply all even numbers followed by all odd numbers (i.e. 2, 4, 8, 1, 3, 5 for n = 6)
- Otherwise, write separate lists of even and odd numbers (i.e. 2, 4, 6, 8 and 1, 3, 5, 7 for n = 8)
- If the remainder is 2, swap 1 and 3 in the odd list and move 5 to the end (i.e. 3, 1, 7, 5 for n = 8)
- If the remainder is 3, move 2 to the end of the even list and 1,3 to the end of the odd list (i.e. 4, 6, 8, 2 and 5, 7, 9, 1, 3 for n = 9)
- Append the odd list to the even list. (i.e. 4, 6, 8, 2, 5, 7, 9, 1, 3 for n=9)
Now, the solution is obtained by placing queens in the rows given by these numbers, from left to right, i.e. a4, b6, c8, d2, e5, f7, g9, h1, i3 for n = 9.
Of course, a single solution can also be obtained as the solution to an Integer Linear Programming problem, which has first been proposed by Hoffman et al. in 1969. The formulation is quite intuitive and simply maximizes the number of queens on the board, while constraining the number of queens on each row, column and diagonal to a maximum of 1. But, being an ILP, this approach does cost an immense amount of computational power, especially for large n.
Significantly more problems arise when one tries to enumerate all possible solutions to the problem for a certain board size. Brute-force algorithms that are commonly used to count the number of solutions are computationally manageable for ‘small’ board sizes such as n=8 or n=10, but would be intractable for problems of n ≥ 20 as the number of possibilities would grow enormously, for example at n=20 one would find possible board positions for 20 queens.
One queen more
The real challenges, though, are extensions of the standard n queens problem. A particularly interesting extension is the problem in which we attempt to place m>n queens on an n-by-n board. Of course, this cannot be done without adding some auxiliary pieces. By custom, pawns are used to essentially ‘hinder’ the queens; the pawns do not have to be unable to capture any other pieces. To find some solution with arbitrarily many pawns is of course a trivial exercise. Consider, for example, Figure 3.

Difficulty in this problem is caused by restrictions on the number of available pawns. Typically, solutions with only one or two pawns can be found. Unlike the standard n queens problem, this is very much an open problem: as of today, no clever algorithms such as the one discussed above have been formulated. For small n, some solutions have been constructed by hand. For example, a solution to the problem of placing nine queens on an 8-by-8 board, using only a single pawn is shown in Figure 4.

Horsey go ‘round
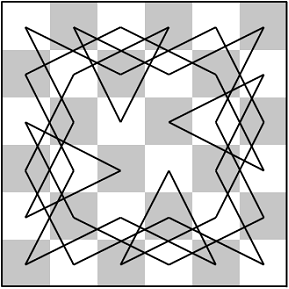
Another very interesting problem is known as the (closed) knight’s tour problem, in which we attempt to find the sequence of moves of a knight that represents a full tour of the knight across the board in such a way that every square is visited exactly once and the knight returns to its original location. To offer some intuition, a solution to this problem on a 6-by-6 board is shown in Figure 5. The open knight’s tour is a little more general in the sense that we do not require the knight to come back to his original position. Typically, the closed problem is considered.
As you might have determined by now, the complexity of this problems quickly spirals out of control: the number of existing open tours for n = 1, 2, … , 8 is 1, 0, 0, 0, 1.728, 6.637.920, 165.575.218.320, 19.591.828.170.979.904. To put that into perspective: for your computer to be able to even be able to store all of the solutions for an 8-by-8 board at the same time, it would need 4.7*10^12 gigabytes of RAM memory, which is much, much more than the 4 to 8 gigabytes of RAM modern computers typically have. However, even though this massive number of solutions exists, you might find it quite difficult to even find a single one, for an 8-by-8 board. So, let us find out how mathematics could aid us in our quest for a solution.
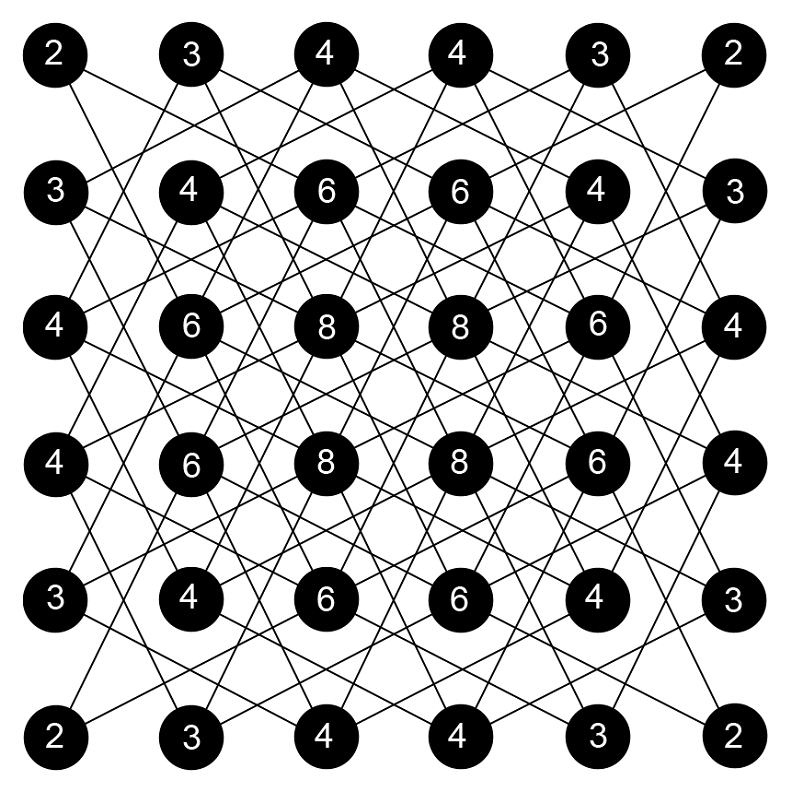
The first useful observation is that the knight’s tour problem is in fact an instance of the Hamiltonian cycle problem. Indeed, given the movement restrictions of a knight from one square to the next, we could construct a graph known as the Knight’s Graph. In this graph, each node represents a square and each edge between two nodes represents the possibility of movement between those two squares. The knight’s Graph for n = 6 is shown in Figure 6. However, unlike the general Hamiltonian cycle problem, this problem has been proven to be solvable in polynomial time.
Many mathematically beautiful approaches to this problem exist. Let us describe a relatively simple heuristic, known as Warnsdorff’s Rule, introduced by H.C. Von Warnsdorff in 1823. The rule states that one should always move the knight to the square from which the knight will have the fewest onward moves. By definition of the problem, previously visited squares should not be counted when calculating the number of onward moves for each candidate square.
It is, of course, possible to have two or more choices for which the number of onward moves is equal; making the ‘wrong’ choice on these occasions could make Warnsdorff’s Rule fail to produce a solution for boards as small as 5-by-5. There are various methods for breaking such ties. Warnsdorff himself proposed to just randomize the choice, which generally works well enough for boards smaller than 100-by-100; for boards of those sizes success rate is almost always above 50%, so simply rolling the dice a few times would usually do the trick. However, for larger board sizes, this approach would generally fail to produce a solution. To solve these larger problems, we would need a more sophisticated tie-breaking-rule, such as one devised by Squirrel and Cull.
Essentially, what Squirrel and Cull propose is to start the process with some (arbitrarily chosen) ordering of the eight basic directions a knight is allowed to move in, and to always prioritize the move highest on that list when two or more are tied for first place. One such ordering would be 12345678, which tells us to always prioritize direction 1 over all others, direction 2 over all but 1, etc. Using this rule once proved to be unsuccessful for small boards (n < 50), but using a cleverly generated sequence of move orderings (12345678, 21345678, etc) and trying each one until a solution has been found proved to be extremely successful: for each of the m-by-n boards with 10 ≤ m,n ≤ 300 they tried, a solution was found within the first nineteen move-orderings.
Another approach is known as the divide-and-conquer algorithm. This algorithm essentially splits up a large board into smaller boards, finds solutions for the smaller boards and the links them together to find the solution for the original board. For the interested reader, a particularly nice paper on this subject is “An efficient algorithm for the Knight’s Tour problem” by Ian Parberry, 1997.
Whether it be bloodthirsty queens looking to capture one another or lonesome knights wandering across the board, mathematics has – as usual – its own ways to tackle the problems at hand. Who knows, you might just be the one to think of clever ways to wield its power and in doing so, you might find yourself retaliating from that first loss as you approach ‘the game of kings’ with a fresh perspective.
References
P Cull and J DeCurtins, Knight’s Tour Revisited, Fibonacci Quart. 1978,
A.J. Schwenk, Which Rectangular Chessboards have a knight’s tour? Math. Mag. 64 (1991)
Parberry, An efficient algorithm for the Knight’s tour problem, Discrete Applied Mathematics 73 (1997)
Text by: Pepijn Wissing



