Improving passenger satisfaction at NS when dealing with wait-depart decisions

November 3, 2015January 5, 2016 Nekst-Online 248 Views

A relatively small train delay can already put a transfer at risk. If a transfer is indeed at risk, two decisions can be made; either the connecting train departs according to schedule, causing some passengers to miss their transfer, or it waits, propagating delay further through the network. The latter option prevents relatively large delays due to a missed transfer. Dealing with these decisions is known as Delay Management.

The Netherlands has an extensive railway network that is highly utilized every day. The main part of this network is operated by Netherlands Railways (NS). NS operates approximately 5,200 trains each day to transport over 1.2 million travelers within the Netherlands. Over the years, NS’ focus has shifted more and more towards passenger satisfaction and the aim to minimize overall passenger inconvenience. Hereby, the general notion that higher delays cause increasingly more inconvenience for passengers is adopted. In addition, due to the high utilization of the railway network, the Dutch government takes special interest in NS’ performance. This interest is also focused on passenger satisfaction and the government requires NS to maintain a high level of passenger punctuality; the percentage of passengers that arrive at their final destination with a delay less than a certain norm. The emphasis of both the government and NS itself on passenger satisfaction is what lead to my thesis topic. During my internship at NS, I was asked to conduct a research that would give NS insight in ways to implement the focus on passenger satisfaction with respect to Delay Management, specifically wait-depart decisions.

Theory

The majority of the research on Delay Management has been focused on solving the Delay Management problem with respect to minimizing total passenger delay. This objective is quite straightforward and only takes delays into account in a linear fashion. Therefore, the theoretical part of this research consists of introducing new types of objectives for the Delay Management problem, such that passenger satisfaction is incorporated.

In introducing the different objectives, we use the notation of Dollevoet et al. [1], because this Integer Programming formulation of the Delay Management problem is used as base model for this research. In this IP formulation, it is assumed that passengers always take the fastest route to their destination. Passengers that share the same origin, destination and starting time of their journeys thus travel exactly the same route and consequently suffer the same delay. Therefore, in order to determine total passenger delay, it suffices to calculate the delay per OD-pair and multiply this delay with the number of passengers that share this OD-pair ( $w_p$ ). The objective of minimizing total passenger delay can thus be denoted by:

(1) $\begin{equation*} \begin{split} \min &\quad \sum\limits_{p \in \mathcal{P}} w_p (t_p - SP_p) \end{split} \end{equation*}$

Here, $SP_p$ indicates the arrival time of a passenger with OD-pair p in the case that there are no delays. $t_p$ stands for the arrival time of a passenger after delays are introduced in the network and corresponding optimal wait-depart decisions are taken. The term between brackets thus indicates the delay suffered by all passenger corresponding to OD-pair p.

The first alternative objective is minimizing the sum of maximum passenger delay. This objective can easily be rewritten such that the corresponding Delay Management problem can also be formulated as Mixed Integer Programming (MIP) problem.

(2) $\begin{equation*} \min \qquad \max_{p\in \mathcal{P}}\ (t_p - SP_p) \end{equation*}$

The second alternative objective is minimizing the sum of all squared passenger delays.

(3) $\begin{equation*} \begin{split} \min \quad \sum\limits_{p \in \mathcal{P}} w_p (t_p - SP_p)^2 \end{split} \end{equation*}$

Finally, we introduce the objective of minimizing the sum of all dis-utilities.

(4) $\begin{equation*} \min \enspace \sum\limits_{p \in \mathcal{P}} w_p f_p(t_p) \end{equation*}$

Where $f_{p}(t_p)$ is a piecewise linear function:
$f_{p}(t_p) = \begin{cases} \alpha_{1p} (t_p - SP_p) + \beta_{1p} \enspace & \text{if } b^0 \leq t_p - SP_p \leq b^1 \\ \alpha_{2p} (t_p - SP_p) + \beta_{2p} \enspace & \text{if } b^1 < t_p - SP_p \leq b^2 \\ \quad \qquad \vdots \\ \alpha_{kp} (t_p - SP_p) + \beta_{kp} \enspace & \text{if } b^{k-1} < t_p - SP_p \leq b^k \nonumber \end{cases}$
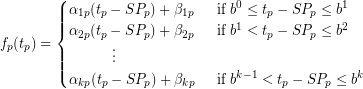
Here, interval i consists of all passenger delays between $b^{i-1}$ and $b^{i}$ . In addition, the $\alpha$ ‘s and $\beta$ ‘s represent the slope and constant term of the linear functions on each interval, respectively. Both parameters can not only differ per interval, but also per passenger. Dependent on the shape of the dis-utility function, different rewriting methods are used to ensure that the corresponding Delay Management problem is a MIP problem.

Data

In order to solve the Delay Management problems that correspond with the introduced objectives, we need data on passenger streams. This is provided in the form of OV-chip card data (OVCP data). This data includes the location and time of passenger check-ins and check-outs and the type of OV-chip card used. Despite the fact that OVCP data can be used to monitor passenger streams, NS cannot link this data to specific individuals. Data of an OV-chip card provides only information on the trip made and the type of OV-chip card, not on the passenger making the trip. The same person traveling twice on the same day is thus seen as a different person and is counted as a passenger twice.

From July 9, 2014, all passengers traveling with NS are obligated to check-in and check-out with an OV-chip card. This implies that almost all passengers traveling through the network are accounted for. Up until now, research with respect to Delay Management at NS has only included data from before 2014. This makes this research highly relevant to NS, as we work with a more accurate view on passenger streams. In addition, using the type of the OV-chip card, we can assign each passenger to one of three main passenger groups: commuters, students and social travelers. Though there is no way of knowing a passenger’s true dis-utility when suffering delay, we can try to estimate such a function for the three passenger groups. This is done using passenger satisfaction grades. We define two types of dis-utility functions; one where passengers are seen on time up until three minutes delay and one where passengers are seen as on time up until five minutes delay. This is in line with the current discussion on what to set as norm for passenger punctuality. At NS an attempt to define a passenger dis-utility function has never been made before, which makes the dis-utility definition in this research another aspect that makes it relevant to NS.

For this research the amount of data available is substantial, due to the amount of passenger that travel by train in the Netherlands every day and the use of the OV-chip card. Therefore only a part of the entire Dutch railway network is considered. Roughly said, the considered network concerns the railway network between the stations at Utrecht, Arnhem, Nijmegen, ‘s Hertogenbosch, Eindhoven and Tilburg. Furthermore, OVCP data on passengers traveling through this network on one specific day was used. Even then, the amount of data is substantial and network reduction techniques have been applied to make it more manageable.

Practice

Ideally, each decision is taken using an exact Delay Management model. However, this is too complex to be used in practice. Therefore we aim to introduce simple rules based on the Delay Management models introduced, such that they can be implemented in practice and perform well with respect to passenger satisfaction.

Multiple trains travel the same trajectory during the day. Think for example about the local train going from Tilburg University to Breda. It departs every hour at 18 and 48 minutes after the whole hour. A transfer thus also occurs multiple times a day. The collective term for all transfers that occur during the day between two trains, is a connection. Figure 1 shows a connection between two trains on a workday, according to the 2015 timetable. For each transfer of this connection, it is indicated up until which time it is optimal for the connecting train to wait. We clearly see that which time is optimal, i.e. the optimal threshold time, differs per objective that is considered. Basing a rule-of-thumb on these optimal threshold times thus gives a rule-of-thumb that is likely to perform well in terms of the considered objective.

First, we consider a rule-of-thumb introduced before by De Lugt [2]. This base rule-of-thumb, the ROT, defines for three threshold times per connection, i.e. three times up until which the connecting train waits for the feeder train. Figure 1 shows a division between the transfers by a dashed vertical line. For each interval, the ROT takes the median of all optimal threshold times and this is the threshold time that applies to all transfers within an interval. Thus yielding three threshold times.

Next, we consider more general rules-of-thumb. The connecting train involved in the transfers displayed in Figure 1 can also be the connecting train for other transfers. One connecting train can thus have different threshold times in the same interval, depending on which feeder train is delayed. We therefore develop new rules-of-thumb, but instead of being connection specific, they are connecting train specific. Put differently, a threshold time of the ROT defines the maximum waiting time of a connecting train for a specific feeder train, while a threshold time of any of the other rules-of-thumb defines the maximum waiting time of a connecting train for any feeder train. These other, general, rules-of-thumb are; MinROT, MaxROT, MedROT, DweightROT and IntWeightROT. The first three take the minimum, maximum and median of all ROT threshold times of one connecting train, respectively. The DweigthROT and IntWeightROT take a weighted average of the ROT threshold times, based on daily or interval occupancy rates respectively. In terms of difficulty in application, the general rules-of-thumb are easiest to apply and the ROT the most difficult. Despite difficulty in application, the ROT is the most specific rule-of-thumb and therefore expected to perform best.

Results

Numerical results in this research have been obtained considering three scenarios. These scenarios entail the presence of a single source delay, two source delays and multiple delays in the network. Based on computation time and overall performance, we find that the Delay Management models with the objectives of minimizing the sum of all delays and the sum of all dis-utilities are most promising. All are expected to perform well when it comes to passenger satisfaction, but using the dis-utility objective can, in some cases, improve performance with respect to dis-utility considerably.

The scenarios that entail more than one delay enable us to compare the rules-of-thumb in a realistic situation. Contrary to our expectations, numerical results show that the ROT does not always perform best. A possible explanation for this is that all rules-of-thumb are based on optimal threshold times, which are based on a single source delay. The fact that multiple delays are present in the scenarios therefore might interfere with performance of the rules-of-thumb. In general, the MaxROT and MedROT are shown to perform second best to the ROT in different scenarios. A possible explanation for the first however is the choice of train series that are delayed. The MinROT perform worst in all cases.

From this research, we concluded that the ROT indeed performs best, though performance of the majority of the other rules-of-thumb is relatively close. Therefore, it is recommended for NS to use general rules-of-thumb, as the much easier implementation goes paired with relatively good performance. Moreover, especially in cases that have a short transfer time, a rule-of-thumb can make much difference as the current policy of NS performs poor here. In order to make a recommendation for which general rule-of-thumb that should be implemented, more research is needed. In particular, more delay cases and scenarios should be considered. Finally, note that though this research is relevant for NS, results cannot be implemented in practice directly. This has to do with a simplifying assumption that is made; the infrastructure capacity is not taken into account when deciding upon which trains should wait and which should depart according to schedule. Though this is a substantial simplification of reality, it was a necessary assumption as including capacity is more of a PhD topic than a Master’s thesis topic.

References
[1] Dollevoet, T. and Huisman, D. and Schmidt, M. and Schöbel, A., “Delay management with rerouting of passengers”, Transportation Science, 46(1), pp. 74-89, 2012.

[2] N. De Lugt. “Delay Management: Improving rules-of-thumb concerning wait-depart decisions”. Master thesis, Tilburg University, 2013.

Text by: Steffie de Roover

Theory

Data

Practice

Results

You May Also Like

Sentiment analysis using Support Vector Machines

Cyclical Patterns and Running Risks

Default Correlation