Calculations to Prevent Chaos
An all too familiar scenario for those interested in crime series on TV: a group of terrorists plans a devastating attack, passing messages to one another in empty apartments in shady neighborhoods. At the exact moment the attack is supposed to be carried out, counterterrorist agencies figure out who is involved and what their roles are; smart computer experts use nifty software to find out who is responsible for placing the bomb, shooting the president or whatever their goal might be and miraculously, they intervene just in time.
As discussed in the Nekst issue of summer 2014, mathematics is used in fighting crime. Here, we take it one step further and show the ways in which mathematics can help in the field of life and death that is counterterrorism. You might have your doubts with regards to the realism of the described TV-scenarios, but one thing we can be sure about is that nowadays a lot of time and money is spent on counterterrorism. Since ever more complex problems call for smarter and smarter solutions, we will show how the elegant field of mathematics can be applied to one of the most uncontrollable and unpredictable problems of modern time, to decide where to spend valuable resources such as money, time and agents.
Breaking their cells
Let us turn to the field of graph theory. Consider a terrorist cell, consisting of terrorists and communication paths. Communication could be done by phone calls, by real-life meetings, via advertisements in newspapers; basically anything you can think of. We model the terrorists by nodes and we say communication between two nodes is only possible if a direct line between these two nodes exists. An example of such a graph is shown in Figure 1. One criterion for disrupting the cell is the connectedness criterion. This criterion states that we can reasonably say to have disrupted the terrorist cell when we have removed one or more nodes (terrorists) such that the graph breaks into two unconnected subgraphs. In Figure 1, removing nodes B and D would result in breaking the terrorist cell. No terrorist strike can be carried out by the remaining terrorists, so we have succeeded. Or have we not?
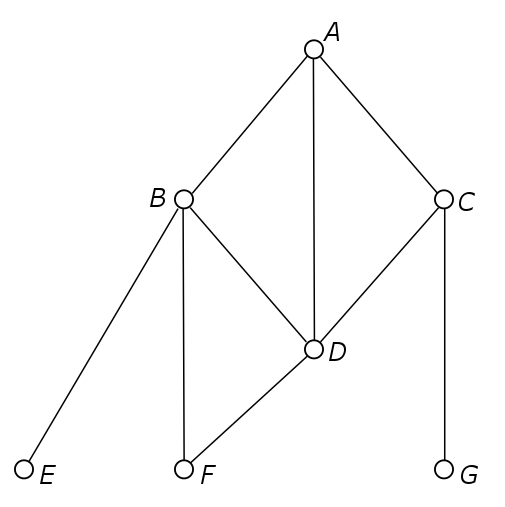
Recent developments in the application of math to counterterrorism suggest that the connectedness criterion is not the right measure. A drawback associated with the use of this measure will be discussed below. It has been suggested that what we need instead of graph theory is the field of mathematics known by the name of lattice theory. Just like in any organization, it is likely that a terrorist organization has a certain hierarchy in its structure. Some members are leaders, others are followers.
Figure 2 shows a partially ordered set (poset), which is the main concept in lattice theory. In the example, person B is higher in the hierarchy than persons E or G, but there is no clear hierarchy between persons E and G. Unlike in normal graphs, the vertical location of a node in a poset graph is actually important, since it gives us information about the hierarchy.
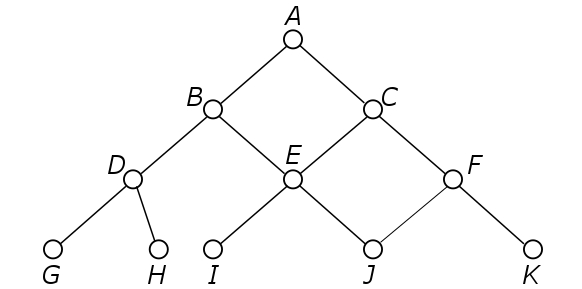
Now, removing persons B and E, for instance, would result in breaking the poset graph into multiple unconnected subgraphs, disrupting the terrorist cell. However, person A can still pass messages to person C and person C can pass messages to person F. Finally, person F can instruct persons J and K to perform some terrorist attack. Even capturing person K as well would not solve this problem, as history has shown that devastating attacks causing many deaths can be carried out by just a single person. It is therefore wrong to assume that breaking a poset graph into subgraphs means that we have made a successful intervention. An alternative criterion is that we have disrupted the terrorist cell if it is unable to pass messages from top to bottom, that is, from the leader to one of the foot soldiers.
Therefore, we would like to capture either person A, persons B and C, persons D, E and C, or any other combination that would cut off leader A from all foot soldiers G to K. In other words, every maximal chain from top to bottom has to be disrupted. An example of a maximal chain is ABEG. A set of nodes which disrupts every maximal chain is called a cutset.
Now, we are getting to the essence of the story. When an intelligence agency captures a number of terrorists, say k members of a cell, they want to know the probability that the cell is disrupted. In other words, they want to know the probability that there is a cutset among those k members. Denote by 
the probability that terrorist cell T is disrupted when k members are captured or killed. If we write 
for the amount of cutsets of size k or smaller in terrorist cell T, we obtain:
where n is the total number of members of the terrorist cell. For Figure 2, the only cutset of size 1 is A. Using combinatorics we find that the total number of cutsets of size 2, 3 and 4 are 11, 56 and 170 respectively. For an effort of capturing 1, 2, 3 or 4 terrorists we are rewarded with a probability of disruption of the terrorist cell of 9%, 20%, 34% and 52% respectively. Thus, if you happen to work for an intelligence agency, two things should be clear to you by now. First, this framework helps you to understand the probability of a successful intervention, when you do not know where the captured terrorists exactly fit in the hierarchy. Of course, in case we know where some of them fit in, our predications will be more accurate. Secondly, the example above suggests that the probability of disruption increases rather quickly in k. Allocating a little more manpower to also capture a fourth member, instead of just three, seems like a reasonable investment.
Practical issues
Keep in mind though, that terrorist organizations do not give away their organizational structure on a silver platter. In practice we unfortunately do not know what poset corresponds to a terrorist cell’s structure. Intelligence sources might be able to tell who the leader is and gain other information about the general structure and size, but unless the captured terrorist was actually planting a bomb, it might be difficult to find out where he or she would fit in. A particular structure that is often encountered is the so-called tree structure.
Let us consider this tree structure. A tree structure has exactly one maximal node, which represents the leader, such as person A in Figure 2. Every other member has exactly one superior. In Figure 2, person E has two superiors, namely persons B and C, so this is not a tree structure. It is unlikely that a terrorist answers to two superiors, because capturing him would put both of them to danger. Our analysis of the tree structure does not stop here though: there are still many tree structures that a terrorist cell can adopt. We shall once again call the concept of the cutset to aid. Naturally, a terrorist cell will want to organize itself in the best possible way. Even though we are not sure whether or not terrorists study lattice theory, it is likely that some of the results are known to them as well, through trial and error. Therefore, by determining theoretically ‘good’ structures, we might just find structures very similar to the ones actually in use. For now, we define ‘good’ structures as being those with few cutsets.
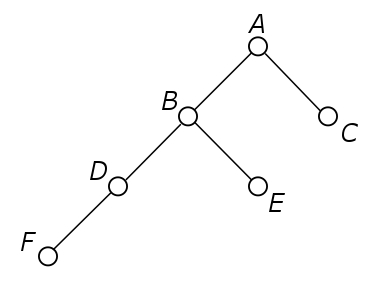
It turns out that, by using advanced mathematics, ‘good’ structures are special pure binary fishbone posets. In this complicated name, binary indicates that each member has at most 2 subordinates (followers). A special pure fishbone poset looks like the graph shown in Figure 3. This also happens to be the ‘best’ binary single leader poset for terrorist cells with 6 members. For 5 members, the graph that is obtained by simply deleting node F is the ‘best’. For smaller terrorist cells, other structures turn out to be even better. The fishbone structure, however, can easily be extended to larger terrorist cells, for instance by giving terrorist D an extra follower. It has not yet been shown that these fishbone structures are the ‘best’ for sizes larger than 6.
What if we are too late?
Ideally, we would get hold of terrorist cells while they are in communication phase and we can prevent them from passing on orders. However, in case plans have already been communicated, capturing terrorists who are no foot soldiers might not make a difference. At this stage, we have to call upon other counterterrorism methods. For fairly obvious reasons, terrorists like to focus their attacks on important and crowded places. The probability of an attack on your house is, luckily for you, not that big. Naturally, focusing our protection efforts on those important places is the way to go. But which places should we protect, and how much should we spend on protection? Even here mathematics can come to the rescue.
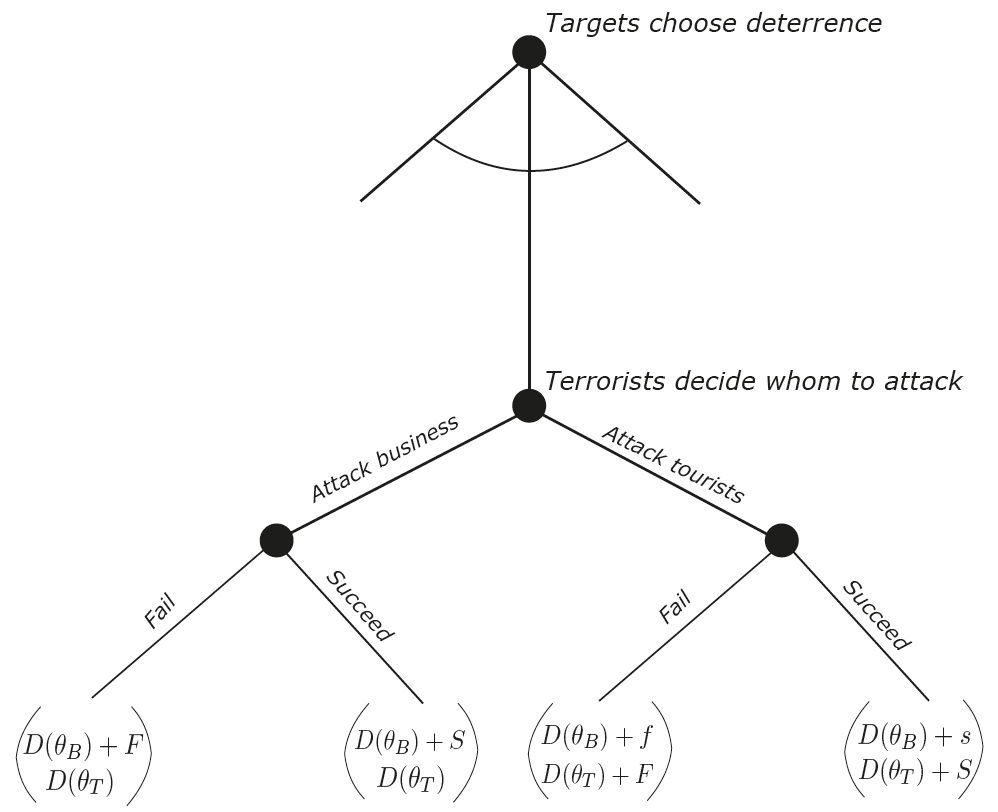
For simplification we shall focus on two places of interest: a business site B and a tourist site T. For both sites, we can choose deterrence or security levels 
and 
resulting in terrorist failure probabilities 
and 
, respectively. Now, which potential target site the terrorists choose to attack is obviously influenced by the level of deterrence at those sites. Say the probability of choosing the tourist site is 
and the probability of choosing the business site is 
, the sum of both being equal to 1. Once the terrorists have chosen their target they launch their attack, assuming that the intelligence agencies did unfortunately not succeed using our lattice theory model from the previous section. For now, we assume they chose the business site. They then succeed with a probability 
. In any case our expected cost involves the deterrence costs . As we econometricians can be very cold-hearted, we assign some cost 
to a successful attack, capturing both damage and casualties at the business location. A failed terrorist strike might also result in some damage, say 
. For simplicity, we say that the damage at the tourist site will also be or , in case the bad guys strike there. However, since business is involved everywhere, it is likely that the business sector also takes some damage in case a tourist site is hit. Thus, in that case, we assign costs 
and 
. A graphical representation of the situation is given by Figure 4.
Smart solutions
Having established all this, important choices have to be made. Both people with tourist interests and people with business interests want their own site to be secure. You can imagine that the more money is spent on protecting the Statue of Liberty, the higher the probability terrorists will go for an attack on Wall Street, because it has become a relatively easier target. Decision makers now have two options: They either cooperate, in which case they minimize the expected total aggregate costs (prevention cost plus damage cost), or they act individually by minimizing the expected cost to their own interest. Let us omit calculations and describe the results. In the case of individually minded decision makers, people with business interests will spend more money on deterrence than that what is socially optimal, i.e. what would have been the result of cooperation. This is due to the fact that their expected loss is higher. However, an opposing factor comes into play. Business interests are also in favor of spending more on tourist site protection, because this also protects their interests at this site. Ironically, this may actually hurt their primary concern: the business site. The models tells us that the tourist site will likely be either overprotected or underprotected, depending on which of the opposing factors described above dominates.
Let us now switch off the mathematic mindset and use some logical reasoning. An ordinary civilian cannot simply call the government and tell them to increase security on a certain monument. Increasing security efforts by means of lobbying, for example, will therefore take some time for tourist sites. Businesses, on the other hand, can act collectively, and protect many employees at the same time. This will lead to underprotection for the tourist site, making it a more vulnerable target to a terrorist attack. If we would use collective deterrence instead, and both sites would decide together on deterrence, total expected costs would be lower. Because this also includes human lives and not just money, this is certainly something to think about. For now, let us just hope that terrorists are not hiding among Nekst readers, and we can continue to use mathematics to our advantage.
References:
- J.D. Farley (2003) Breaking Al Qaeda Cells: A Mathematical Analysis of Counterterrorism Operations. Stud. Confl. Terror., 26, 399–411.
- J.D. Farley (2007) Toward a Mathematical Theory of Counterterrorism. The Proteus Monograph Series, vol 1, issue 2.
- T. Sandler, D.G. Acre (2003) Terrorism and Game Theory. Simulat. Gaming, 34, 319-337.
Text by: Stefan ten Eikelder
