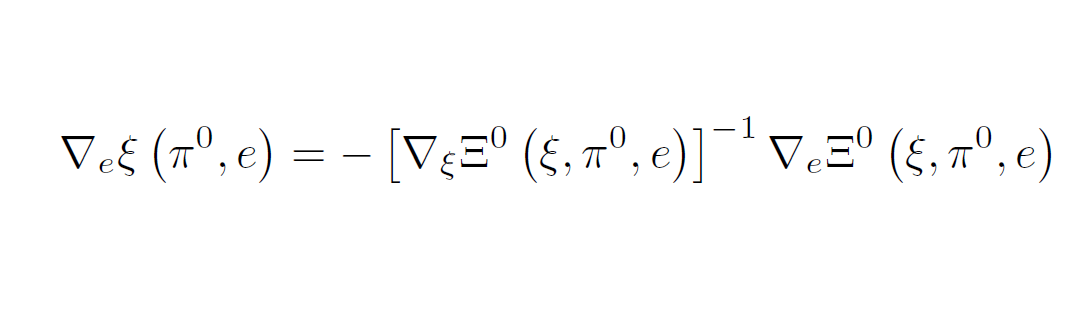Nonparametric Identification of the Sharing Rule in Collective Models with Heterogeneous Agents
Collective consumption and labor supply models have become increasingly popular in family economics. Although the availability of datasets with information on intra-household allocation of consumption is increasing, it is still a challenge to identify structural components of the model, especially if one allows for unobserved heterogeneity. In this essay I will present a general approach how such a problem can be approached in a nonparametric way.
Consumer decision making has always been a central component of economic analysis. Hence, modeling of consumer demands in terms of marginal utility has a very long tradition dating back to the early contributions of Jevons, Menger and Walras in the late 19th century. In the 1930’s their theory was formalized by Hicks and Slutzky to the standard indifference-curve based approach we use now. It was Richard Stone in 1954 who estimated the first system of demand equations. All these endeavours laid the groundwork for the neoclassical framework we use today in order to model household decisions and estimate consumer demands. However, this unitary approach suffers from one important drawback: it assumes one utility function per household, disregarding any interaction between the households’ members. In his seminal work, Chiappori [1],[2] introduced the collective household consumption model, which satisfies methodological individualism by allowing every member s ∈ IS of the household to have his or her own utility function. Household utility can then be viewed as an aggregation rule or social choice function. It is assumed that this social choice function satisfies the Pareto-efficiency axiom, which allows us to write household utility as a linear combination of individual utilities us and define the optimization problem as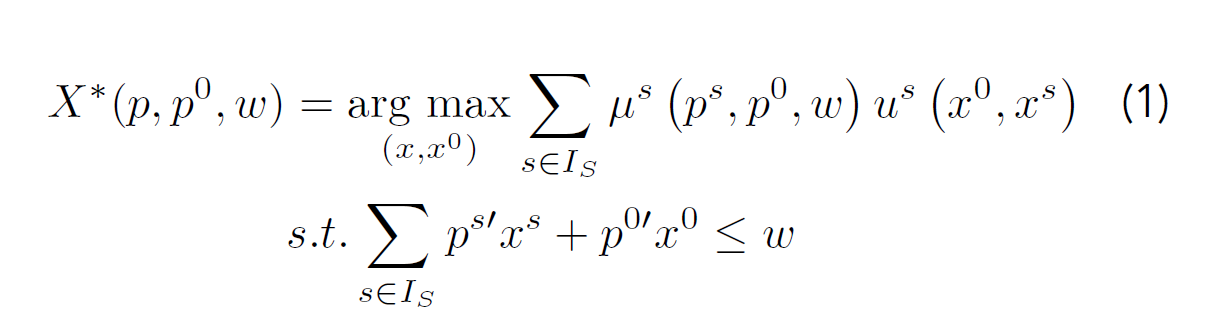
with Pareto weights μs representing the members’ bargaining power, endowment w and prices p =(p1,…,pS) and p0 for privately and publicly consumed goods (x1,…,xS) and x0, respectively. We denote the number of non-restricted privately and publicly consumed goods by L1 and L0, respectively.
Before we solve this collective household optimization problem, let me briefly discuss the issue of demand estimation. After all, as econometricians we are interested in the empirical content of the model. So far we have not talked about any form of unobserved heterogeneity ε. We implicitly assumed that every household has the same underlying utility functions and Pareto weights. If that was the case, every household would attain the same optimum X* (demands) for given (p, p0, w). It is generally accepted that this restriction does not hold, since group statistics still exhibit a significant amount of variation in almost any domain of application. A rather ad-hoc way this issue is usually dealt with, is to first solve the model as if there was no unobserved heterogeneity and then include an additive error term ε in the demand equation that is estimated: X* (p, p0, w, ε) = X(p, p0, w) + ε. The problem with this approach however is that even within the scope of the standard unitary model it is very hard to find a utility function that, when optimized under a budget constraint, would result in a demand function which has such an additively separable form. In general, a stochastic demand system that admits a broad class of underlying utility functions, turns out to be non-separable in the error term(s) ε. Fortunately, there are techniques (see [4],[5],[6]) that allow us to estimate even non-separable functions, however they must satisfy certain regularity conditions. To be more specific, X* (vector-valued) must be monotone and triangular with respect to ε. If this is the case, we are able to identify conditional quantiles of the (components of) demands, by exploiting one of their equivariance properties, the invariance with respect to monotone transformations. Now, since X* is only the solution of the consumers’ problem, we have to investigate which properties does the underlying structure Ω := (μs, us)s∈IS have to satisfy in order for the solution to be of such a form. To answer this question we have to solve problem (1) and use the first order conditions, which define X* in terms of functionals of Ω (system of partial differential equations) to establish restrictions how unobserved heterogeneity ε has to enter Ω such that X* satisfies the desired properties.
In order to solve the model, it will be handy to follow Chiappori [3] who shows, that under the efficiency axiom it is possible to rewrite program(1) as an equivalent two-step procedure, in which the members agree on the sharing of total household income as well as consumption of public goods in the first stage and then, conditional upon this outcome, privately optimize individual consumption. In formal terms this means that there exists a map (p, p0, w) ↦ ρs, the so-called sharing rule, such that every X*(p, p0, w) that solves (1) is also a solution of the following two-stage optimization process. Using indirect individual utilities vs from the second stage, letting πo := [po, p, w], in a first stage the household optimizes
In the second stage, all members s ∈ IS of the household individually optimize, conditional upon optimal public consumption x0 and the sharing rule ρs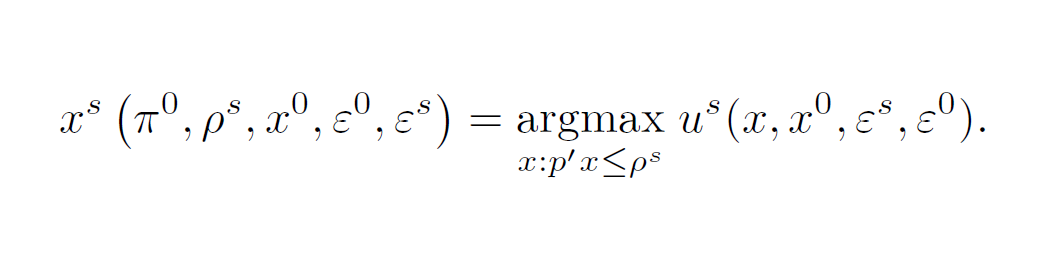
Note that we have also added unobserved heterogeneity into our model structure by defining a vector of random variables (εμ, εo, ε) where εμ represents an S-dimensional vector of unobserved bargaining powers, εo unobserved taste shocks for public goods (L0-dimensional) and ε= (ε1, … ,εS)unobserved taste shocks for private goods for each member s ∈ IS (each L1-dimensional).
We are interested in estimating the (stochastic) demands, which represent the solution of the respective stages. The focus lies on the sharing rule ρ which allows us to investigate not only the aggregate effect of a policy on the household, but also how it is passed on to each member. In general however, a distinction between public and private demands is not possible in many datasets. It can be shown that under such circumstances we can not identify the sharing rule if we allow for unobserved heterogeneity. For this reason, we have to restrict ourselves to datasets that include information on intra-household allocation, which allow us to separately estimate individual private demands xS and public demands and the sharing rule (x0, ρ).
It is easy to see, that in general the solution of the first stage program depends on unobserved bargaining power, public taste shocks (εμ, εo) and private taste shocks ε, whose dimensions are S + L0 and S*L1 respectively, while the number of equations in the system (x0, ρ) is only L0 + S. In the presence of such excess heterogeneity, triangularity of the demand system with respect to the error terms, cannot be satisfied. To overcome this, we will exploit information from the second stage by first predicting ε, using demands for private goods xS for all s ∈ IS. It can be shown that we can then in a second step consistently estimate demands for public goods and the sharing rule conditional upon these predictions of ε, once we have shown that xS is identified. Hence, only (εμ, εo ) is unobserved and we were not required to make an assumption on the structure. As for the individual demand systems in the second stage, we can treat εo as a household fixed-effect and are left with unobserved εs.
Now, how can we link the demands (x0, ρ) and xS to the underlying structure? Without explicitly solving the model, let Ξ0(ρ, x0) = 0 and Ξs(xS) = 0 for all s ∈ IS be the first order conditions of the two stages and define ξ := (ρ, x0) and e := (εμ, εo). Using the implicit function theorem, our first stage demand system, in which public consumption and the sharing rule are allocated can be represented as
in a neighborhood of πo. Similarly, each members’ private demands can be written as 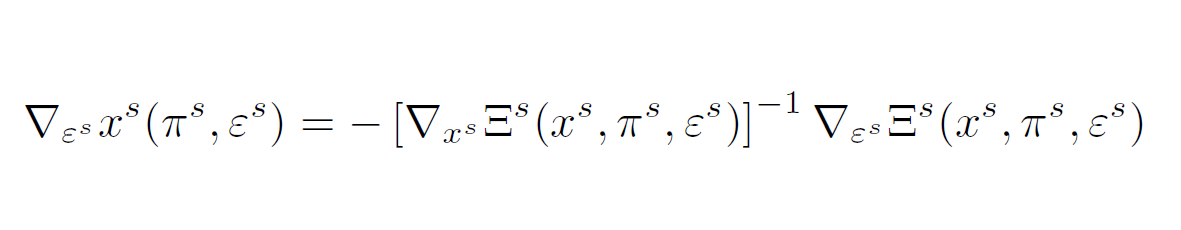
around some πo := (ps, ρs). Note that the existence of the two inverses follow directly from the rationality properties of the individual utility functions. But more importantly, triangularity and monotonicity of ξ and xS are satisfied if and only if their Jacobian with respect to the error terms is non-zero for all πo and (ps, ρs), respectively. As we can see, that is if ∇eΞ0(ξ, πo,e) and∇esΞS(xS, ρs, ε) both have full rank. These restrictions are defined in terms of our first order conditions, which consist of functionals of the underlying structure Ω. Hence we get a set of economically traceable restrictions which, from a mathematical perspective, constitute mostly weak separability conditions. If we are willing to impose these conditions, we can then non-parametrically estimate conditional quantiles of the central structural component of the collective model, the sharing rule. This allows for a range of applications for example to estimate the effect of a policy on the welfare of each spouse or to construct a test that can empirically distinguish the standard unitary model from the collective model.
References
[1] P.A. Chiappori, 1988, Rational Household Labor Supply, Econometrica, 56, 63-90
[2] P.A. Chiappori, 1992, Collective Labor Supply and Welfare, Journal of Political Economy, 100, 437-467
[3] P.A. Chiappori, 2009, The Microeconomics of Efficient Group Behavior: Identification, Econometrica, 77, 763-799
[4] A. Chesher, 2003, Identification in nonseparable models, Econometrica 71, 1405–1441
[5] R. Matzkin, 2003, Nonparametric estimation of nonadditive random functions, Econometrica, 71, 1339–1375
[6] G. Imbens and W. Newey, 2009, Identification and estimation of triangular simultaneous equations models without additivity, Econometrica, 77, 1481–1512
Text by: Stefan Hubner