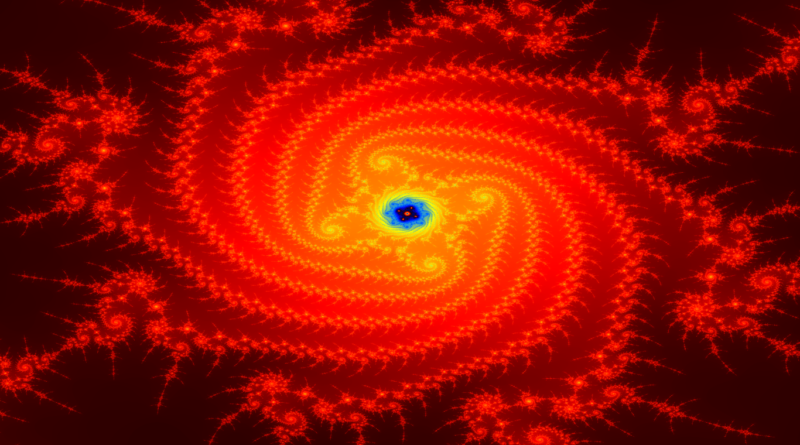
The Mysterious Mandelbrot Set
It is rarely the case that something is easier than it looks. However, in my opinion, the Mandelbrot set is the perfect example. For those who have never heard of it: the Mandelbrot set is a fairly simple recursive formula resulting in a complex symmetrically evolving structure that will even intrigue people that are not particularly interested in math.
The basics
Before we get into the specifics, let us start off with a crash course on complex number theory. Complex numbers extend the concept of the one-dimensional real number line to the two-dimensional complex plane , using the horizontal axis and the vertical axis for the real part and the imaginary part, respectively. All complex numbers are coordinates on the complex plane and can be written as ![]() , where
, where ![]() is called the imaginary unit and
is called the imaginary unit and ![]() .
.
It was Leonhard Euler (1707-1783) who introduced the imaginary unit ![]() , widely known as the cornerstone of complex number theory and complex analysis, and Carl Friedrich Gauss (1777-1855) was the one to introduce the term ‘complex number’.
, widely known as the cornerstone of complex number theory and complex analysis, and Carl Friedrich Gauss (1777-1855) was the one to introduce the term ‘complex number’.
Complex numbers can be used to solve cubic equations or quadratic equations with negative roots, which are undefined for the set of real numbers. If it had not been for complex number theory, the Mandelbrot set would never have been discovered in the first place, as the complex plane is actually the ‘canvas’ of the Mandelbrot set.
Now the foundation is clear, we can move to the fun part: the actual Mandelbrot-set (M-set) itself. The M-set is a fractal: a geometric structure defined by its expanding symmetry. Fractals make use of recursion, which results in a detailed pattern that repeats itself. It was Benoît Mandelbrot (1924-2010), who extended the notion of theoretical fractional dimensions to geometric patterns in nature. Yes, mathematics in nature, you read that correctly. We will discuss that some more, later in this article.
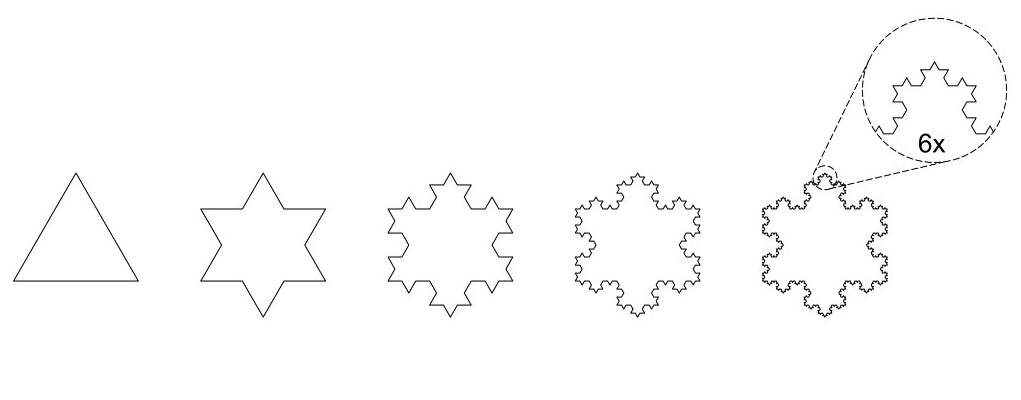
Fractals
A basic and famous fractal is for example the Koch Snowflake, which is shown in Figure 1. As any fractal, its starts with a basis which will, after recursively applying a transformation, reveal a self-similar pattern at any scale. However, the Mandelbrot set, although created by relatively easy mathematics, results in a much more complex symmetrically evolving structure.
What about this relatively easy mathematics? It all comes down to the recursive formula ![]() , defined as
, defined as ![]() , where n is a natural number, c is a constant complex number and
, where n is a natural number, c is a constant complex number and ![]() . As you can see, the equation is using its output as the input of the next iteration. From this, a sequence of complex numbers arises which starts at the origin, by definition. From our analysis course we all know a thing or two about sequences and the M-set is defined as the set of complex numbers of which the sequences obtained by the formula is bounded. In other words, complex numbers c of which the sequence
. As you can see, the equation is using its output as the input of the next iteration. From this, a sequence of complex numbers arises which starts at the origin, by definition. From our analysis course we all know a thing or two about sequences and the M-set is defined as the set of complex numbers of which the sequences obtained by the formula is bounded. In other words, complex numbers c of which the sequence ![]() turns out to diverge to infinity as n → ∞ are not included in the Mandelbrot set. However, constants c of which the corresponding sequence
turns out to diverge to infinity as n → ∞ are not included in the Mandelbrot set. However, constants c of which the corresponding sequence ![]() converges to a finite (complex) number, or constants c such that
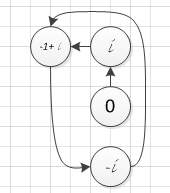
converges to a finite (complex) number, or constants c such that ![]() will keep repeating (part of) itself are contained in the M-set. For example, the so called Misiurewicz-points, named after the Polish-American mathematician Michal Misiurewicz, are dense in the boundary of the M-set, which means that for any boundary point of the M-set the epsilon neighborhood of that point contains at least one Misiurewicz-point. Without getting into the specifics, we will provide two Misiurewicz-points; their periodic behavior is shown in Figure 2 and Figure 3. The two points are are
will keep repeating (part of) itself are contained in the M-set. For example, the so called Misiurewicz-points, named after the Polish-American mathematician Michal Misiurewicz, are dense in the boundary of the M-set, which means that for any boundary point of the M-set the epsilon neighborhood of that point contains at least one Misiurewicz-point. Without getting into the specifics, we will provide two Misiurewicz-points; their periodic behavior is shown in Figure 2 and Figure 3. The two points are are ![]() and
and ![]() . The first results in the pre-periodic sequence
. The first results in the pre-periodic sequence ![]() and the sequence of the latter is
and the sequence of the latter is ![]() .
.
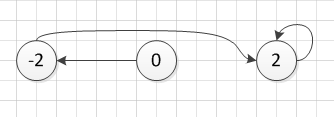
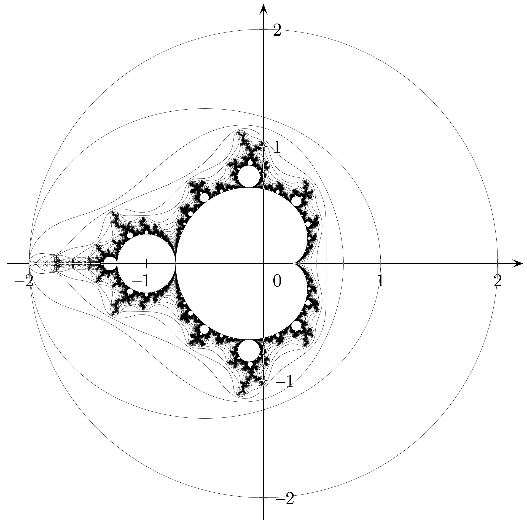
It turns out that the collection of complex constant numbers c that meet the requirements for the Mandelbrot set remain within the circle with radius 2 and its center on the origin of the complex plane, as shown in Figure 4. Therefore, the complete Mandelbrot set is included in this circle. Hence, being a fractal, the M-set is infinitely self-similar and it contains detailed mathematical constructs. Zooming in on the Mandelbrot set will reveal new generations: cute, little babies, no matter at what scale it is looked at. This explains why the M-set was not discovered until the 19th century, even though the necessary complex number theory had already been discovered two centuries before that: modern computers were needed to perform the iterated calculations on the complex plane.
The M-set mostly owes its fascinating appearance to the varying use of color ranges. The coordinates in the complex plane that belong to the Mandelbrot set are often colored black. I am sorry to say that it is actually the coloring of the coordinates that do not belong to the M-set that results in the most marvelous pictures. This is because these are often assigned color ranges that depend on the number of iterations after which the sequence is known to be unbounded. For some sequences this only becomes clear after more than 1500 iterations. Because of the differences in the number of iterations needed before this becomes clear, beautiful, lively colored swirls and frills are revealed: the Mandelbrot set in its true glory. When you open up your imagination, the M-set is not only a mathematical structure, it becomes art. Its shape will remind you of numerous things. Seahorses (Figure 5), a Buddha (Figure 6), lightning bolts, leaves, trees and many more.


Fractals in nature
As I mentioned before, it was professor Mandelbrot that linked theoretical fractional dimensions to geometric patterns in nature. From now on I promise you, you will not be able to not see the fractal symmetry in nature. Just to get the creativity flowing, I will provide you with some examples. For the vegetable lovers: buy a Romanesco broccoli, but do not get so fascinated that you forget to eat the thing. After my example of the Koch Snowflake, ice crystals and snowflakes will probably already have crossed your mind. But also air bubbles, water drops and fossils are examples of fractal symmetry in nature. The beauty of mathematics in nature, you just cannot escape it! Admittedly, as an Econometrics student, you might already have known this. What you probably do not know is that fractals are used to predict patterns in nature, which helps us to sharpen low resolution images, as can be seen in Figure 7. The thing is, fractal algorithms can sharpen your pictures without making them look over processed, because it actually is adding sharpness and not just pumping up the contrast or anything like that. In addition, it is insensitive to digital artifacts in your photos, because it really looks for patterns.

I think I covered the most interesting aspects of the Mandelbrot set, but for the interested reader, I highly encourage you to take a look at the Mandelbrot set zoom video below. But watch out, an epilepsy/seizure warning might be in order.
References
O. Merino, A Short History of Complex Numbers. University of Rhode Island (2006)
S. Gunther, 14 Amazing fractals found in nature. www.mnn.com (accessed on February 12, 2016)
http(1): www.prodigitalsoftware.com/dslr_fractal_sharpen.html (accessed on February 12, 2016)
http(2): www.en.wikipedia.org/wiki/mandelbrot_set (accessed on February 12, 2016)
Text by: Steffi van den Hanenberg