Traveling Sales Rock Star
Being a salesman in the 1800s, traveling from city to city to try to sell goods for a living, does not seem like a very rewarding job. It might indeed not have been, but the job itself has lent its name to the Traveling Salesman Problem (TSP). The recipe for an infamous problem baffling scientists for decades is actually quite simple: despite being very easy to formulate, TSP is extremely hard to solve. On the upside, we can use it to plan holidays and understand animal behavior.
People have been solving TSPs since long before the problem has been formally formulated. Any animal or human being has the tendency to minimize the distance that has to be covered when, for example, collecting food from multiple locations. Back then, covering more distance cost more energy and led to an increased risk of encountering a predator or being later than competitors, but nowadays, TSP’s applications are mostly used to increase profits. Mathematicians W.R. Hamilton and Thomas Kirkman were the first ones to mathematically formulate the problem in the 1800s. More than a century would pass until the first attempts to solve it were made. During the 1950s, the RAND Corporation started to award prizes for notable contributions towards solving the problem. For those not familiar with the problem, it can be described in one sentence: ‘Given a collection of cities and the cost of travel between each pair of them, the Traveling Salesman Problem asks to find the cheapest way of visiting all of the cities and returning to your starting point.’
Pushing the boundaries
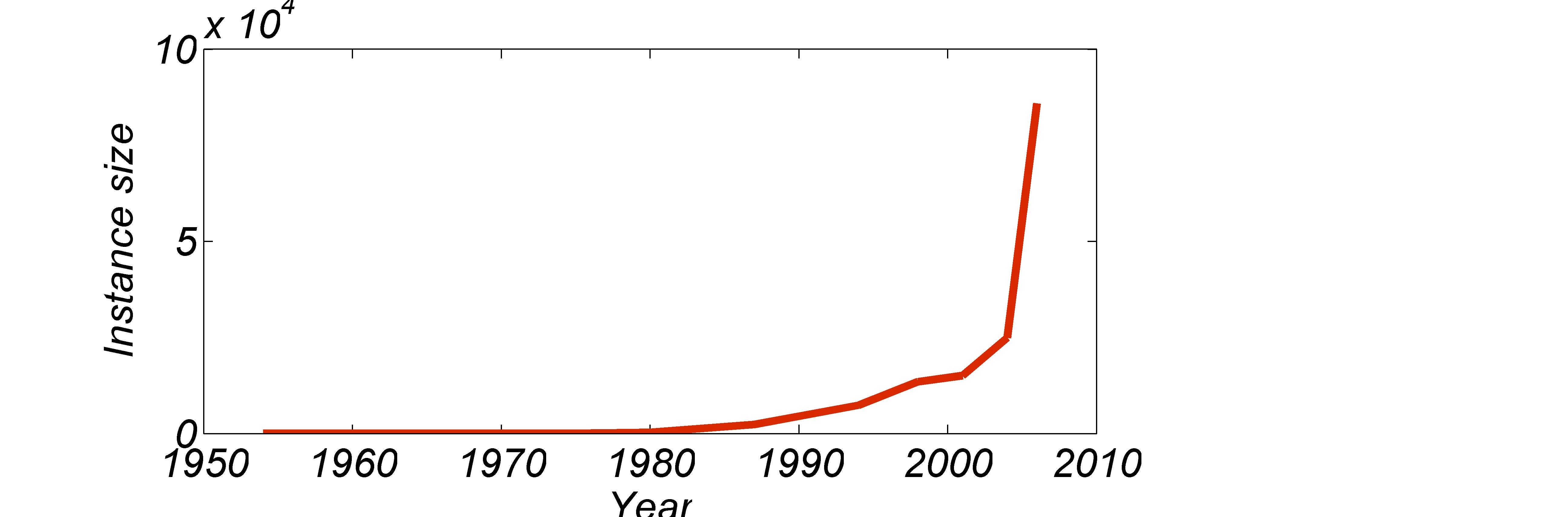
The Traveling Salesman Problem is a so-called NP-hard problem. Without going in to the underlying complexity theory, it is important to mention that we do not have a polynomial-time algorithm for solving the general case of the TSP, meaning we cannot easily solve large instances to optimality. And, possibly also interesting, in case you would find such an algorithm, you have actually solved the infamous P versus NP problem: a Millennium Prize Problem rewarding you $1,000,000. Although that has not happened yet, and perhaps never will, scientists have pushed the boundaries further and further, solving an even larger instance to optimality every once in a while. Techniques that are employed for this include the cutting-plane method, the branch-and-bound algorithm and dynamic programming. Figure 1 shows these milestones1; the largest solved instance has 85,900 nodes (or cities if you like) and was solved in 2006. Of course, there are many other problems that are equally hard to solve, but the TSP has long ago claimed the position of most well-known problem: it even has a movie named after it (see box below)
The 2012 movie Travelling Salesman considers four mathematicians hired by the US government to solve the P versus NP problem. Perhaps you could refer to this movie to explain what life as an econometrician is like?
A mathematical holiday
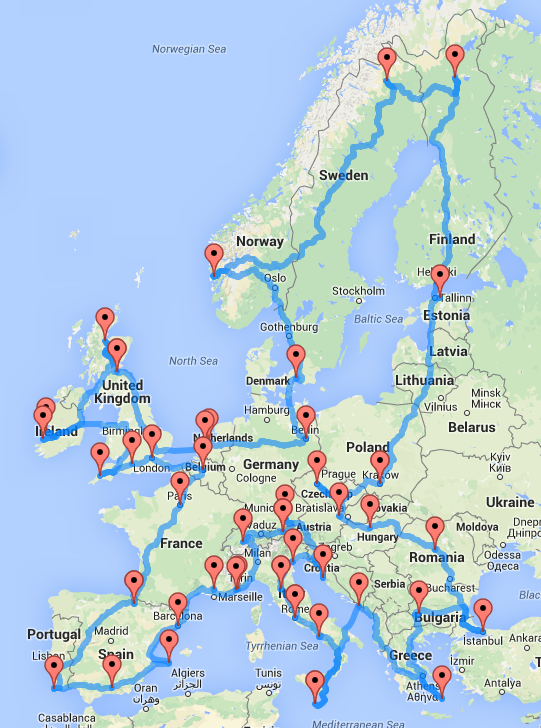
Most problems in mathematics do not acquire the fame of the TSP, let alone having a movie named after them. One of the reasons for this is that its applications are numerous and easy to understand. An important example in industry is drilling holes in computer chips. If the routes for the drilling machines are shorter, time is saved and therefore money is saved. However, when discussing your studies or work on a party, this is not particularly the example you would want to use to impress others. Perhaps people would be more interested if you discuss your road trip through the 45 must-see-places in Europe? Now, that is of course a typical example of a TSP, and the American Dr. Randal Olson thought it would be nice to actually compute what such a route would look like2. The first problem he encountered was that in order to minimize the length of the tour, one would need to know the distance of direct travel from every landmark to each other landmark. Smart econometricians like you know that one could simply put that information in a distance matrix, which can be obtained using Google Maps API without too much effort. Given all those distances, the total number of possible (valid) routes adds up to a grand total of approximately 1.3 x 1054 possibilities (general formula (n-1)!/2). I guess that your first reaction would be: “I do not want to be the one to check all those routes.”
Even though we do not have an exact polynomial-time algorithm for TSP, and trying out all possibilities is indeed not an option, we do have many heuristics that can be applied to obtain (very) good approximations of the optimal solution. Popular methods include tabu search, simulated annealing, genetic algorithms and ant colony optimization. For illustration, using heuristics the current best tour across all 1,904,711 known cities and towns in the world is at most 0.0474% longer than the optimal tour (a lower bound is known). Returning to our road trip, Figure 2 shows the obtained route using a genetic algorithm. The route has a total length of 26,211 kilometers. The code for the algorithm (in Python) is available on Olson’s website, as well as an instruction manual for the Google API part, so you can see if you can improve his route or simply plan your own trip.
The elastic band approach
Most progress discussed so far involved smart people thinking really hard, using sophisticated algorithms and a lot of computer power. What if we take a step back and let nature give it a try? It is generally accepted that evolution has done some pretty amazing things and it is not without a reason that methods based on behavior observed in nature, such as genetic algorithms and ant colony optimization, are used to provide near optimal solutions to many complex problems. Let us first consider human performance on TSP. If you are given a piece of paper with a small number of dots on it, say four, you will likely figure out quickly how to connect the dots into a closed tour such that the total distance is minimal. For larger problems, such as fifteen nodes, you might not be able to find the optimal solution, but will certainly find something that is acceptable. Studies on Euclidean (‘normal’ distances satisfying the triangle inequality) TSPs have shown that even for a 120-city problem, humans construct tours that are on average only 11% longer than the optimal tour.
This begs the question: What techniques do humans employ when faced with a TSP instance? First of all, humans tend to look at the convex hull of the set of points under consideration. The convex hull can easily be visualized by taking an elastic band, and stretching it around the outermost nodes such that all nodes are included. Nodes that touch the elastic band are on the boundary of the convex hull, and apparently putting more nodes on this boundary does not lead to a higher complexity for human participants in experiments. It turns out that humans often connect the nodes on the boundary, and then make a sequence of the remaining nodes in the interior, subsequently inserting this somewhere in the original tour.
An alternative hypothesis is that humans instinctively try to avoid crossing arcs, reportedly occurring in only approximately 6% of solutions. For a Euclidian TSP, an optimal solution can indeed not contain crossing arcs, so this is not just an aesthetically pleasant strategy. A solution approach that suits this hypothesis is the hierarchical nearest neighbor process. Participants often make small clusters of nodes, and solve these clusters independently, using a nearest neighbor strategy while avoiding crossing arcs. These clusters are then connected to one another using again a nearest neighbor approach on a global level. This again produces a tour that, at first glance, seems reasonable.
Bumblebee grand prix
Let us omit the neuropsychological details to these approaches and briefly discuss how animals solve TSPs. Yes, animals solve TSPs too: elephants walking from water pond to water pond will not take the recreational route and bees foraging different flowers optimize their routes too. In October 2010, UK newspaper The Guardian wrote an article titled ‘Bees’ tiny brains beat computers, study finds’. Referring to the TSP, they state that ‘bees can solve complex mathematical problems which keep computers busy for days, research has shown’. Although that is a bit misleading, for all we know bees have not actually written a polynomial-time algorithm for solving the general case of TSP, the research did reveal that despite a brain the size of a grass seed, bees perform surprisingly well on small scale TSP instances. When eight bees were confronted with six different artificial flowers, they used an average of 10.75 different routes (out of 720 possibilities). Six bees used the optimal one as their primary (most used) route after approximately 26 foraging bouts, while the other two selected it as their secondary route.
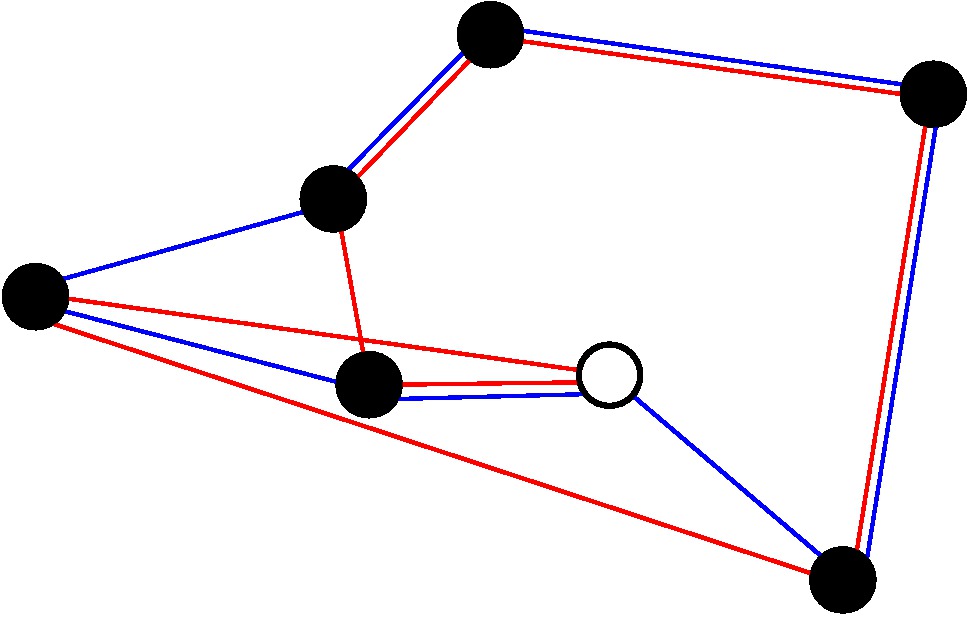
These results already seem rather impressive – remember we are talking about bees, not monkeys – but gets even better. The experiment was designed in such a way that using a nearest neighbor (NN) heuristic would result in long tours. An example of such an instance is shown in Figure 3. Starting from the white node, an NN heuristic would give the red route, but the blue one is clearly better. It can be concluded that bees do not apply an NN heuristic, but some other method. It is clear that bees employ their spatial memory, and keeping track of multiple locations at the same time. At the time of writing, it is unclear exactly which other methods are used. One possible hypothesis states that the bees try to keep a consistent directionality of movements; making a very sharp turn at a node is usually not the best idea. This approach again leads to a circular route and the remaining nodes can be incorporated using trial and error. After all, that is nature’s approach to anything. This method is actually very similar to the convex hull approach discussed before, which is remarkable because the human participants in the experiment had a nice overview of the nodes on paper, while the bees certainly did not.
Many more experiments considering the fascinating traveling salesman problem have been executed, involving chimpanzees, amongst others. The experimenter carried the animals past eighteen food locations, in a random order. Upon release, the chimpanzees followed a near optimum path through the eighteen locations.
Whether you would like to plan a road trip or test the problem solving skills of your guinea pig (or indeed your pet bee), the traveling salesman problem offers many nice applications. The rock star of combinatorial optimization can even reward you a nice prize, but we like the challenge, not the money, right?
References
- http://www.math.uwaterloo.ca/tsp/index.html
- http://www.randalolson.com/2015/03/10/computing-the-optimal-road-trip-across-europe/
- http://www.theguardian.com/world/2010/oct/24/bees-route-finding-problems
- J.N. MacGregor, Y. Chu. (2011) Human performance on the traveling salesman and related problems: a review. J. Probl. Solving, 3, 1-29.
- Lihoreau, L. Chittka, S.C. Le Comber, N.E. Raine (2012) Bees do not use nearest-neighbour rules for optimization of multi-location routes. Biol. Letters, 8, 13-16.
Text by: Stefan ten Eikelder




