Special: Mathematics & Love
Over the past Nekst editions, we have dealt with numerous topics concerning mathematics. We have considered math in the field of arts, sports, crime, etc. However, one matter we have not yet discussed is mathematics combined with love.
When thinking about the concept of love, one will probably not associate it with any form of science, let alone mathematics. As it turns out though, there are numerous ways in which this emotion has to do with mathematical approaches. Are you wondering how many partners you should have had in order to select the best one? Have you ever wondered how dating sites determine who is your ‘perfect’ match? And why do we perceive some people as more handsome than others? In this article we will explain how our most beloved discipline is used in the world of love. It might even help to sort out your own love life!
The secretary problem
Let us start with an easy example. Imagine having to find a new secretary for yourself and say that there are one hundred applicants. You can interview all of them, in any order you want, but the catch is that you have to make a decision about the candidate right after interviewing him/her. Once rejected, the participant cannot be recalled. It is obvious that choosing the first applicant will most likely leave better ones still un-interviewed, whereas choosing the last applicant probably results in having dismissed a better one already. So then, what is the optimal strategy? After having interviewed how many applicants should you choose your secretary?
As it turns out, the magical number in this secretary problem, or often called the marriage problem, is 37. The rule of thumb for such a situation involves giving each and every applicant a different score. After having interviewed 37 participants, one must choose the first applicant who scores higher than any of the ones before. This optimal stopping solution uses the rule n/e, where n equals the amount of applicants. In fact, no matter what value you take for n, as long as n is big enough, the probability that you have found the best candidate is about 37%.
So where do this rule and percentage come from? In order to find this answer we have to dive into the more mathematical part of the problem. First we will consider the dilemma for n equal to 100 again. Let k-1 be the amount applicants you will certainly pass by before choosing the one better than any of his predecessors. Then for any applicant up and until k-1, we have no probability of having chosen the best secretary (as we never choose these). When we choose the k’th candidate, we simply have a chance of 1/100 of having selected the best one. For the applicant k+1 this number is the same, but we have to keep in mind the risk that we might already have chosen the wrong candidate at k. Therefore, the probability of choosing the best contestant at k+1 becomes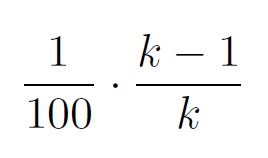 
as the best contestant so far must be in the first k-1 (for it must certainly not be the k’th candidate). Now for k+1 we find a probability of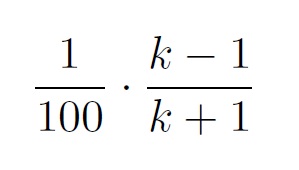 
Therefore, the stopping formula equals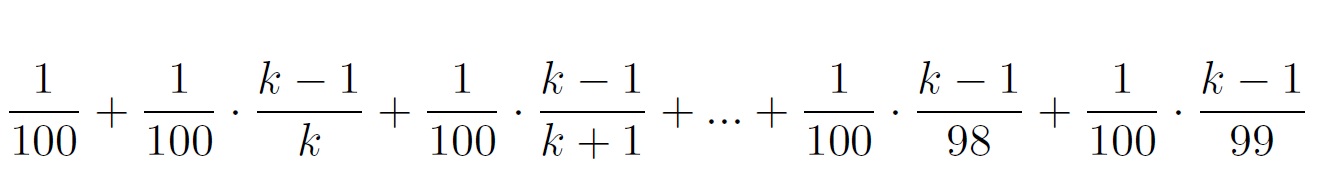
Now if we expand this to the more general form, where we have n contestants, we find the formula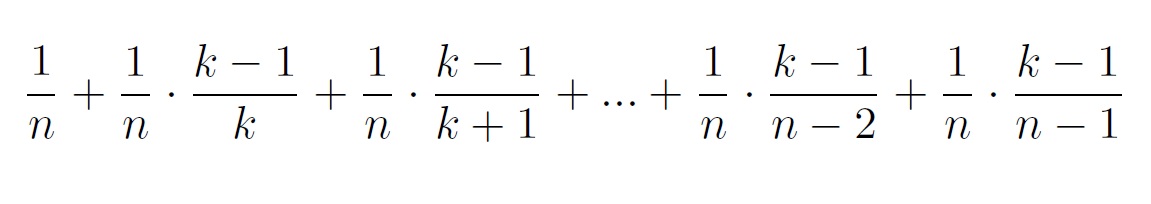
which we can write as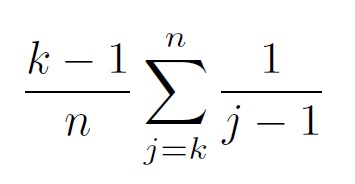 
The graph for n =100 is plotted here and we find that the maximum value is located at 38, which indicates that we have to let 37 (so k-1) applicants pass. From this we can conclude that, firstly, the optimal cutoff point tends to n/e as n increases, and secondly that for large n the best applicant is chosen with a probability of 1/e ≈ 37%.
Real life
We have now figured out that the optimal cutoff point for the secretary problem with one hundred applicants equals 37. However, this dilemma does not seem too familiar to our day-to-day lives. After all, we do not have only a hundred possible partners to choose from, nor can we grade each of them distinguishably. However, the German psychologist Peter Todd adapted the general strategy such that it discards the principle of finding the sole best contestant. Instead, he assumed that anybody would be happy with a partner who is in the top ten percent, but would want a probability of at least 75% to find such a partner.
Todd calculated that the optimal amount of candidates/partners for this problem equals twelve. After twelve partners, you should stay with the first one who is better than any of the others you have been with. However, Todd does not define the concept of a partner. As having at least twelve long-term relationships might be hard to accomplish for most of us, it might be better to also include one-night stands, crushes, or anything you think counts for you.
For people who are already having a hard time finding a partner at all, let alone twelve, online dating sites are the place to be. The internet is becoming more and more popular in order to find somebody’s significant other. In fact, over 13%[1] of the couples that started living together over the past five years have found each other via the internet. Therefore also more and more dating sites are making their entrance, all using different algorithms. While most agencies use a questionnaire to retrieve information of their users, there are also sites that take a different approach. The site Soul2Match for instance, matches users via their photographs. The company GenePartner on the other hand uses a formula to match men and women by analyzing specific genes in their DNA. The American site HowAboutWe solely relies on user’s ideas for a (first) date. Anyone interested in your idea can simply connect and the two of you are off on a date!
If you want to know more about this topic, it might be interesting to watch the episode ‘Hoe vind ik de ideale partner’ from the Dutch show Eureka. In this program, Sofie van den Enk and Ionia Smeets use mathematics to answer difficult problems. The episode can be found on Uitzending Gemist.
Dating sites
Match.com’s algorithm
A site that does use its very own algorithm to match people via a questionnaire is match.com. Even though most of the precise steps of the algorithm are unknown, as other dating agencies might listen along, some tricks are in fact known. The site started in 1995 and brought on Amarnath Thombre as the VP of the department strategy analytics. His team consists of twelve loyal workers, which include some mathematic PhD’s. Together they have implemented a new algorithm, which has resulted in a massive increase in the number of subscribers.
When subscribing to Match.com, the first thing you have to do is fill out a survey about yourself. The most basic part of their suggestions results simply from matching people with similar characteristics. However, you have to take into account that the information of the subscribers might not be (completely) correct. People often claim to have a higher salary and/or IQ, and at the same time conveniently underestimate their waistlines. Besides, the preferences of users regularly deviate from what they have entered. For instance, you might state that you want a partner from within your own town, but still look often on profiles from outsiders. Therefore, Thombre’s algorithm uses the following idea: pay more attention to the choices users make on their site than on what they say they want. “Instead of trying to create the perfect algorithm, we try to create the perfect algorithm for you,” Thombre says.
The site also looks at users with the same behavior as you. It considers people with whom your behavior has interacted with to be more likely matches for you. This is another way of determining what you like even if you cannot express it.
Big data
Over the past 19 years, Match.com has evidently collected a vast amount of data. The team has thereby documented hundreds of correlations, such as:
- Republicans are more likely to reach across party lines to contact a Democrat than vice versa.
- A woman who smokes daily is less likely to email a man who does not smoke.
- Women of “other” religions show positive propensity to email a Jewish man.
Whether all this data analysis actually pays off and will match you to your perfect partner, is still unclear. “We do not pretend to know who is right for you, but we use mathematics to quickly learn how your complexity shows itself on the site,” Thombre says. “We are like a bartender who is always observing particularly which types of people are talking to each other and hitting it off.”
Beauty
In our other ‘Mathematics & …’ specials, we have already established that the golden ratio phi can be found in almost anything. We have found the number in flowers and plants, in pine cones, music, paintings, architecture and so on. As it happens, this section plays again a big role in our definition of beauty. It has long time been stated that having the golden ratio implemented somewhere in your face makes you more attractive. However, in almost every face such a proportion can be found and many scientists therefore believe that it is only a myth that the golden ratio makes you more beautiful.
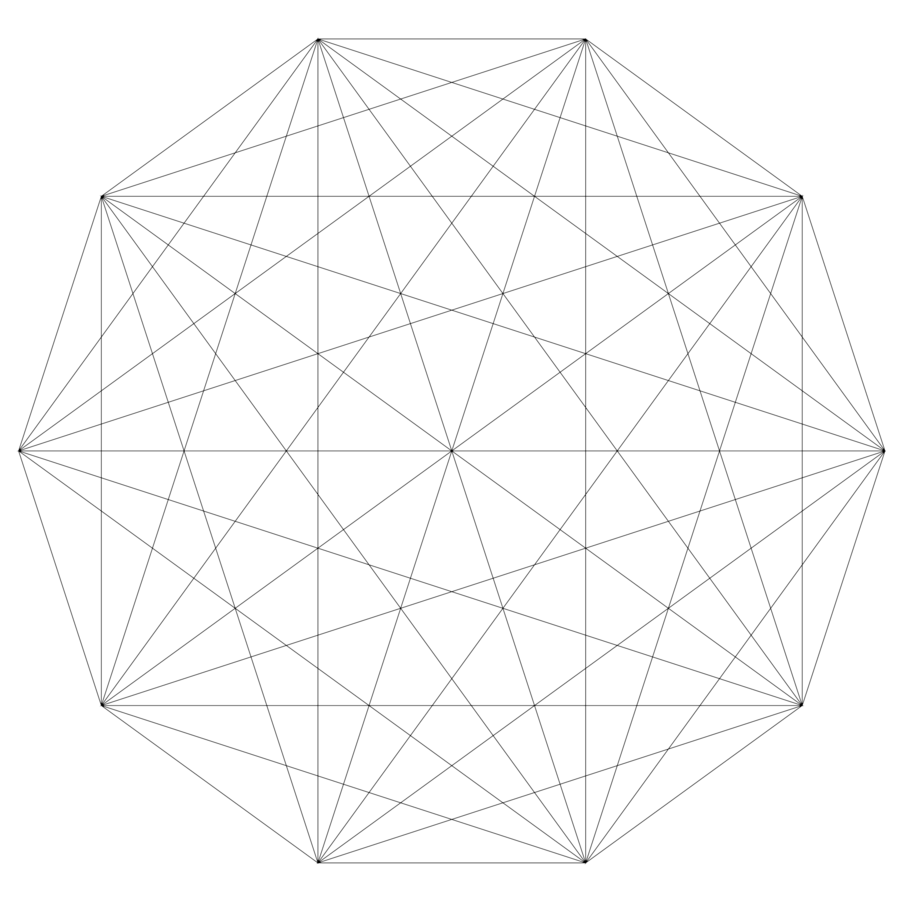
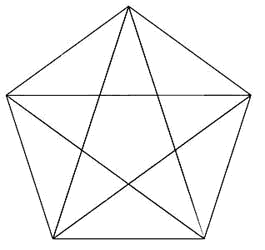
Stephen Marquardt on the other hand, does truly believe in the geometrically perfect face and has constructed the ‘Phi Mask’. In order to do this, Marquardt made use of The Golden Decagon Matrix (Figure 1). This matrix is constructed by connecting two lines of 1.618 units (phi) and a 1.000 unit line, such that you find an isosceles triangle, called the Acute Golden Triangle. When we add two Obtuse Golden Triangles, we have created the Golden Pentagon (Figure 2). Now if we duplicate this pentagon and rotate it 36°, we find the Golden Double Star Complex , whose vertices can be connected to form the Golden Decagon Matrix. Marquardt used this Matrix to create the Phi Mask, which supposedly outlines the geometrically perfect face (Figure 3).
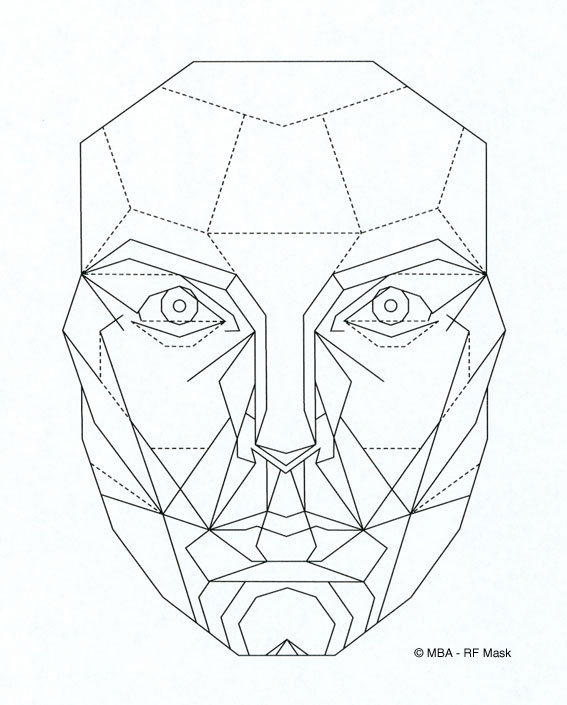
As research demonstrated the level of correlation between a human face and the Phi Mask was directly proportional to the level of perceived attractiveness, many have found this mask convincing, including cosmetic surgeons. Figure 4 shows an example of the beauty mask being applied in Photoshop, with some convincing results.
However, some flaws can also be found. For instance, the mask is apparently ill-suited for non-European populations and it only best describes the facial proportions of masculinized white women as seen in fashion models. As scientists continue to discuss about this subject, there is only one conclusion that can yet be made: beauty is relative. It differs for every sex, ethnicity, and age group. Therefore, if your face does completely mismatch with Marquardt’s mask, do not feel miserable. You might very well still be beautiful!
Conclusion
Once again we can conclude that mathematics is omnipresent in our world. Scientists all over the globe are trying to find formulas, algorithms, and techniques to approximate human behavior towards love. As we have already come a reasonable way, it is safe to say that mathematics can help us in this field as well. However, much more time and research is necessary if we want to dive deeper in the scientific version of love. After all, love is a subjective matter.
Bibliography
http://en.wikipedia.org/wiki/Secretary_problem
https://www5.cuhk.edu.hk/oge/oge_media/gef/doc/best_works/1st_bestwork/dorothylaw.pdf
http://www.npo.nl/eureka/24-10-2013/KRO_1644527
http://www.beautyanalysis.com/index2_mba.htm
http://www.goldennumber.net/beauty/
[1] Source: CBS, http://www.datinginsider.nl/cbs-steeds-meer-mensen-vinden-relatie-via-internet
Text by: Ennia Suijkerbuijk
