Where Math and Art Meet
Mathematics have emerged after humans intuitively started to observe, measure and record Mother Nature’s amazing phenomena. In addition to this, daily requirements like food sharing and agricultural division and more general tasks like time recording, seasons change, and building a habitat caused mathematics to rise in use. The human being has linked mathematics slowly to his everyday life needs, such as organizing irrigation canals in agriculture, building dams, and constructing ships, using the rules of geometry, volumes, and numbers. Humans paid attention to what nature suggests in terms of harmony and congruency of phenomena, namely, the shape of mountains and flora, music from the wind, rain, waterfalls and rivers. The facts suggest there is a tight relationship between mathematics and nature, beauty and art.
A Link with Nature
The harmony and exactitude of components in nature lead to think that mathematics has played a role somewhere. Whenever there is precision, there is mathematics involved. It is enough to contemplate nature to notice the repetition of certain shapes, called fractals. Fractals are spirals that can be viewed in the heart of a daisy flower, in the leaves of a plant called fern, but also in DNA and hurricanes. Fractal design has become a trend in painting as well, where the same shape is reproduced or magnified, mimicking the natural fractals. Mathematicians have attempted to describe fractals and one way they succeeded is trough Mandelbrot sets. The book titled ‘Chaos and Fractals’ by Peitgen, Jürgens & Saupe provides a thorough introduction to those who would like to know more about fractals.1
From another perspective, one cannot approach art in nature without considering the famous golden ratio. This ratio appears particularly in round and curved shapes, just like fractals. If one looks closely, snail shells and elephant tusks are quite similar in the way they are curved. This is because they obey the law of the golden ratio. The human body also follows the golden ratio since, for example, the ratio of the index finger length to the hand length is equal to the ratio of the hand length to the arm length. Even plastic surgery uses the golden ratio.
Mathematics and Music
As Pythagoras rightly said: “Everything is shaped following a number; beauty itself is based on metrics, the origin of the world is a number and a sound; mathematics and music”
Pythagoras was the first to find a relationship between the length of a string and the sound it produces – also known as acoustics. Scientists have come to the conclusion that music uses mathematics such as addition and logic which appears in musical notations. For example there is a half-step between the note (mi) and (fa), (si) and (do), and a full step among the other notes. Classical contemporary music is a mathematical study of frequencies that music instruments produce. Furthermore, there is a similarity between the note scale and mathematical series.
In particular, some arithmetic reflections are to be found in music compositions. The best example found is the Fibonacci sequence, named after the Italian medieval mathematician, Leonardo de Pisa alias Fibonacci . As we know, the first two numbers are 1, and every new number is the sum of the 2 preceding numbers. We obtain (1, 1, 2, 3, 5, 8, 13, 21…). What is interesting is that the ratio of two successive numbers converges, again, to the golden ratio, φ = 1.61803398.
A study by Garland (1995)2 shows that the golden section also appears in melody lines. An example is the Hallelujah chorus in the oratoria Messiah, by Handel. The whole piece consists of 94 measures and the entrance of solo trumpets “king of kings” is played in measure 57 to 58; after about 8/13th of the whole piece (which is equal to 0.6154). After 8/13th of the first 57 measures, i.e. measure 34, the theme ‘’the kingdom of this world’’ kicks in, another essential point in the chorus. Again after 8/13th of the second 37 measures, the entrance “and he shall reign” takes place. However, there is no argument that Handel actually used Fibonacci sequence or the golden number in his composition; he probably created a harmony that made sense to the ears and mind.
Mathematics and Architecture
The human need for order and harmony finds its root in the need for survival. For this purpose, humans sought ways for continuity and safety, and therefore they built houses based on geometry and metrics. Man excelled in housing decoration by designing shapes and drawings of all styles and dimensions. This is the case for the Egyptian pyramids, the Babylon tower, the Parthenon of Athens, but also Mayan and Aztec temples, Arabian and Persian mosques, and last but not least do not forget Pisa tower in Italy. As the great German artist Albrecht Dorr pointed out: ‘’geometry is the one science that can depict reality in a deep manner.” The direct usage of mathematics in architecture is naturally, geometry.
Mathematics and Sculpting
Since architecture and painting are both based on mathematics, it makes sense to assume so is sculpting. This is indeed the case, whether it is a rock or wooden sculpture – such as Arabesque – mathematics has a role to play. Geometry is crucial here to guarantee overall beauty and harmony of shapes. The golden ratio is used extensively. Euclid, the Greek father of geometry, righteously claimed that: “harmony is the twin of beauty”, and where harmony is present, precision follows, and therefore, mathematics.
Classical artists do not actually consider mathematics when they apply or perceive a golden proportion. The effect of beauty and harmony is so evident that no explicit measurement is needed, it becomes an intuitive process for the artist or sculptor. The act of sculpting is more of a mental process of geometrization and abstraction rather than an actual measurement.3
Nowadays, there is an artistic field called mathematical sculpturing, that produces sculptures that are explicitly drawn from mathematical geometric figures. There are geometrical sculptures; where we find some works of the 20th century movement that is called Cubism, relying on the cube as a theme for sculptures. Besides that there is the polyhedral sculpture type that produces beautiful and simple pieces that look like polyhedrons, or semi-regular polyhedrons. There are also non-Euclidean geometries that use elliptic and hyperbolic geometries to produce a piece of sculpture. And finally, of course, there is the fractal geometry that shows evolving replications of a certain shape. 4
Mathematics and Painting
If one observes the paintings by famous artists in the era of the European Renaissance such as Michelangelo and Fra Angelico, one would see a relationship with mathematics in the sense that there is a concordance between volumes, color spectrum, luminosity degree, and the choice of lines. In the Mona Lisa, Leonardo da Vinci also did a great job in harmonizing the dimensions of the body especially in the face, which is a common technique for the “portrait”.
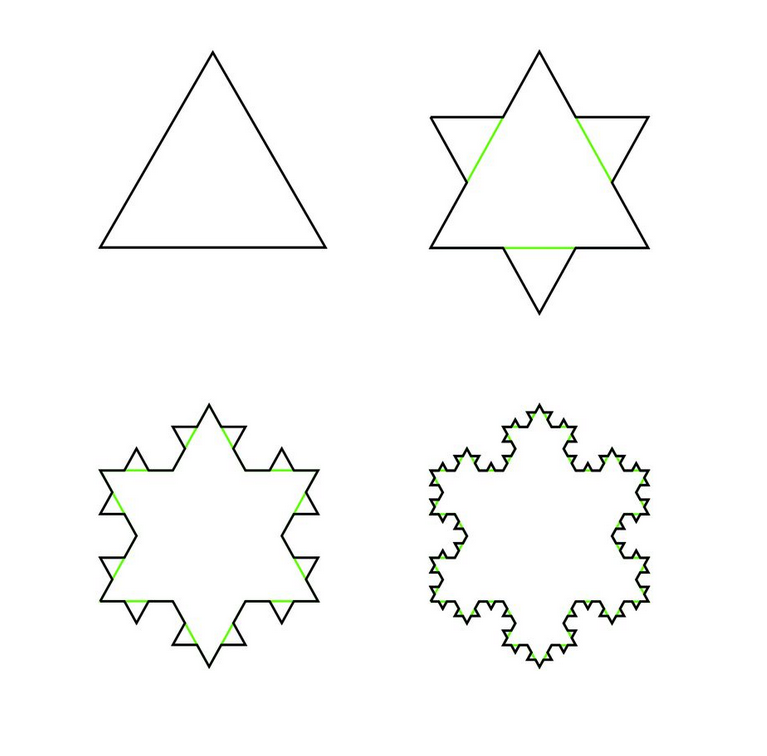
Von Koch Snowflake
Here we present an example of how to make a nice drawing using the principle of fractals.
The Von Koch snowflake is a fractal which is constructed from an equilateral triangle as follows:
1. Remove the middle third of each side
2. Build a new equilateral triangle on each of the resulting gaps
3. Repeat steps 1 and 2 for the new object
If you keep going on indefinitely, you end up with the fractal shown below.
The outline of the snowflake is incredibly crinkly. In fact, it does not contain any straight line segment at all: the middle third of any line segment has been replaced by two sides of a triangle, creating a spike. Mathematicians measure the crinkliness of a fractal by the fractal dimension, a generalization of our ordinary notion of dimension. The outline of our snowflake is too crinkly to be one-dimensional. On the other hand, it clearly is not two-dimensional either, since it contains no area. In this case, the dimension lies between 1 and 2, in fact it is equal to log(4)/log(3) = 1.2619.
Conclusion
All in all, mathematics are omnipresent in all types of art. It is also clear that mathematics have wide applications in every part of life. Design of houses, parks, bridges, they all follow mathematics and physics. Although arts use the right side and mathematics uses the left side of your brain, both have a creative aspect to them. Both disciplines are creative endeavors with analytical components that are essential elements of contemporary civilization. Mathematical formulas and geometric figures can be aesthetically pleasing themselves. That is why several mathematicians consider mathematics to be an art and not merely a science. Physicist Wolfgang Pauli said: “It is more important for an equation to be beautiful than exact,”6 suggesting an aesthetic appreciation of what is implied by the mathematical statement of cause and effect.
In my personal opinion, I believe that the greatest mathematical findings were based on inspiration, which is a right brain process, such as Archimedes’ Eureka. I view mathematics and arts more like the yin/yang symbol, they are one in two, and two in one. •
References
1. http://fractalfoundation.org/category/natural-fractals/
2. http://www.pages.drexel.edu/~jjn27/mathandmusic.pdf
3. http://www.mi.sanu.ac.rs/vismath/barrallo1/
4. http://pages.towson.edu/gsarhang/67%20-%2074.pdf
5. http://plus.maths.org/content/artmathx
6. http://staff.washington.edu/rockne/math-art.pdf
Text by: Maha Lharoui