Cyclical Patterns and Running Risks
In order to absorb losses from, for example, defaulting loans, banks are required to hold capital reserves. In the Netherlands, requirements for the level of capital reserves are based on the capital requirements as described in the Basel capital accords. In order to determine capital requirements banks provide input parameters. However, different philosophies underlying the determination of those input parameters might lead to different capital requirements.
In 1970, the Basel Committee on Banking Supervision (BCBS) was established. This committee is responsible for guidelines on the supervision of banks worldwide. Since its establishment, BCBS has generated several international regulatory standards, referred to as Basel I, Basel II and Basel III. In the latest accords, BCBS aimed to make capital requirements more risk sensitive. Hence, banks are required to determine input parameters that are representative for the amount of risk taken. These parameters are the exposure at default (EAD), loss given default (LGD) and probability of default (PD). Capital requirements are determined on the basis of these parameters. When looking at a portfolio of (retail) loans, the input parameters are to be determined for a bucket of loans with similar characteristics. Hence, capital requirements are calculated per bucket. Total capital requirements are obtained by summing the capital requirements per bucket.
The Vasicek Model
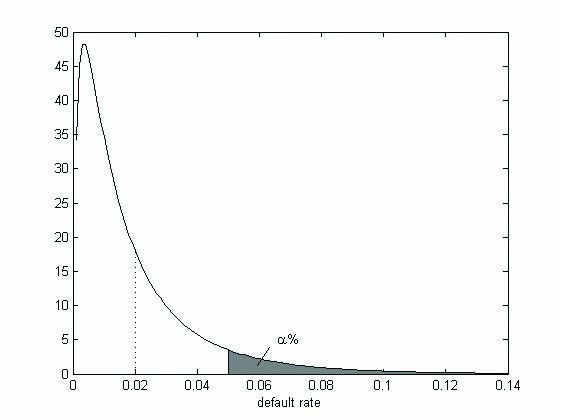
Underlying the capital requirement formula described in the Basel capital accords is the Vasicek model. By the Vasicek model, the probability that a loan defaults depends on an idiosyncratic factor as well as a systematic factor. For example, the idiosyncratic factor could be influenced by illness or a divorce, while the systematic factor could be influenced by houseprices or wages. Hence, the systematic factor influences the probability of default of the entire portfolio, while the idiosyncratic factor only influences the probability of default of one obligor. Because the default event of a loan depends on a systematic factor, the number of defaults in a portfolio does not necessarily converge to the expected default fraction, when the number of loans in the portfolio goes to infinity. Instead, a default fraction distribution can be determined, referred to as the Vasicek distribution. We arrive at the capital requirement formula described in the Basel capital accords by determining the 99.9% Value-at-Risk of the Vasicek distribution.
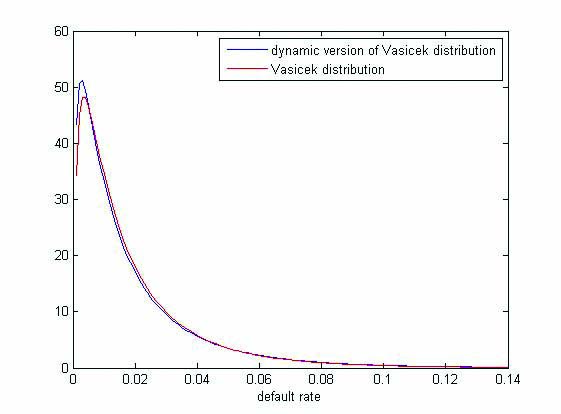
The Vasicek model is a single period model. Hence, it is unable to properly model default events over time. However, the research question covered in my thesis requires a methodology that is able to model default events over time. Therefore I developed a dynamic version of the Vasicek model. There are two important properties that should be satisfied by a methodology modeling default events over time. First, as explained in the Vasicek model, default events are subject to a systematic risk factor. Second, the probability that a loan defaults depends on the state of the economy (see e.g. Crook and Bellotti, 2010). To incorporate these properties in a model, I extended the Vasicek model. Thus, within the framework of the Vasicek model, I assumed that the probability that a loan defaults depends on the state of the economy. In particular, if the economy is in a downturn, the probability of default is higher than during times with normal economic conditions. On the other hand, if the economy is in a boom, the probability of default is lower than during times with normal economic conditions. In all three possible scenarios, the probability of default depends on an idiosyncratic factor as well as a systematic factor. The resulting default fraction distribution is similar to the Vasicek distribution, but it has a fatter tail. Hence, the 99.9% Value-at-Risk is higher.
 Rating Philosophy
Rating Philosophy
Although extensive regulations regarding capital requirements are set in place, there are no explicit prescriptions regarding the philosophy under which the input parameters should be determined. In my thesis, I investigated the implications of different philosophies regarding the determination of the probability of default. We can distinguish two different philosophies: through-the-cycle and point-in-time. The through-the-cycle philosophy is defined as the philosophy where the probability of default is determined over the entire economic cycle. Hence, the probability of default does not depend on the state of the economy. On the other hand, under the point-in-time philosophy the probability of default does depend on the state of the economy. Note that, in the model described above, we made use of three different probabilities of default for three different states of the economy. Hence, the probability of default under the through-the-cycle philosophy equals the expected probability of default, which we set equal to the probability of default under normal economic conditions. Furthermore, the probability of default under the point-in-time philosophy equals the probability of default associated to the current state of the economy.
Also note that, as the probability of default under the through-the-cycle philosophy does not depend on the state of the economy, there is no correlation between the economy and capital requirements. However, as the probability of default under the point-in-time philosophy is higher in an economic downturn and lower in a boom, capital requirements under the point-in-time philosophy are negatively correlated to the economy. This is an important observation, as it leads to procyclicality in the capital requirements. Capital requirements are said to be procyclical if they amplify economic conditions. This can be seen as follows. When economic conditions deteriorate, risk goes up and thus capital requirements go up. In order to satisfy capital requirements, banks will have to attract money. However, since it is expensive to attract money in periods of economic distress, banks may reduce lending. This causes household spending to drop, thereby amplifying economic distress. A similar reasoning can be applied for economic booms. The reduction of procyclicality was one of the objectives in Basel III, underpinning the fact that procyclicality is believed to have important implications for the economic climate. Hence, procyclicality seems to be an important disadvantage of the point-in-time philosophy.
Transitions
However, in our analysis thus far, we ignored the transitions of loans between different buckets within the —› portfolio. As mentioned before, capital requirements are calculated for different buckets and total capital requirements are obtained by summing the capital requirements per bucket. Hence, even though the probability of default per bucket under the through-the-cycle philosophy stays the same over time, total capital requirements might change. This change is due to a different distribution of loans over the buckets. In particular, under the through-the-cycle philosophy an economic downturn, and hence an increase in risk, is reflected by a shift in the distribution of loans towards the worse buckets. In contrast, under the point-in-time philosophy, the distribution of loans does not necessarily has to change due to an economic downturn. Indeed, an increase in risk is already reflected by an increase in the probability of default of all buckets. Hence, we define two different versions of the point-in-time philosophy: the version where the distribution of loans depends on the state of the economy and the version where the distribution of loans does not depend on the state of the economy.
Transitions of loans between different buckets can be modeled by means of a transition matrix. A transition matrix describes the probability that a loan transitions from one bucket to another. However, in a similar fashion as under the Vasicek model, we would like the transitions of loans between different buckets to depend on a systematic risk factor. Furthermore, in order to make the distribution of loans dependent on the state of the economy, we need that transitions between buckets depend on the state of the economy. This idea is supported by empirical observations, as e.g. Nickell et al. (2000) find that transition matrices depend on the state of the economy. Hence, I extended the dynamic version of the Vasicek model to model transitions between buckets.
Results
To compare the different philosophies underlying the determination of the probability of default, I calculated total capital requirements under all three philosophies (through-the-cycle, point-in-time where the distribution of loans depends on the state of the economy and point-in-time where the distribution of loans does not depend on the state of the economy). Note that the following results are sensitive to the choice of the parameters in the model.
Total capital requirements under the through-the-cycle philosophy are, on average, higher than total capital requirements under either version of the point-in-time philosophy. However, total capital requirements under the point-in-time philosophy fluctuate more over time. Although high capital requirements are more likely to give a good protection against future losses, they might lead to a low return on capital. Indeed, capital reserves cannot be used to invest in risky opportunities generating a high return.
Furthermore, total capital requirements under both versions of the point-in-time philosophy are negatively correlated to the economy. This correlation comes from the fact that the probability of default depends on the state of the economy. In contrast, total capital requirements under the through-the-cycle philosophy show a small positive correlation to the economy. This correlation comes from the fact that transitions between buckets depend on the state of the economy. Note that, in theory, we would expect a negative correlation due to a shift in the distribution of loans. Hence, our findings are different from what we expected. A negative correlation between total capital requirements and the economy leads to procyclicality, which is an undesirable property. Hence, in this aspect, we find that the through-the-cycle philosophy has an advantage over the point-in-time philosophy. •
References
Bellotti, T. and Crook, J. (2010). “Time varying and dynamic models for default risk in consumer loans”, Journal of the Royal Statistical Society: Series A (Statistics in Society).
Nickell, P. , Perraudin, W. and Varotto, S. (2000). “Stability of rating transitions”, Journal of Banking & Finance.
Vasicek, O. (1987). “Probability of loss on loan portfolio”, KMV Corporation.
Text by: Elske Leenaars




