Econometric Modeling for Strategic Workforce Planning
Bringing mathematics in the boardroom
“How will my workforce be distributed over the different seniority levels in ten years? Will my company have to deal with redundant employees? How does the demographic aging affect my staff population? What kind of interventions will ensure that our average seniority level increases?”
These are just a few of the questions that might keep a Human Resource (HR) manager awake at night, and many organizations are keen to know the answers to these questions. But how to quantify staff flows? How to quantify the impact of possible management interventions? A workforce optimization model could support in HR executive decisions on strategic workforce planning. We built a model to answer the questions raised above: The Business Simulator.
Due to, amongst others, the difficult economic climate and aging of the population, workforce prediction modeling is becoming a hot topic, especially for organizations with large, comprehensive workforces. These organizations wish to quantify their HR strategy, but generally do not have technically trained employees to substantiate and quantify the desired future solidly. Looking into the HR software market we found to our surprise that most software developers only build static models with less focus on modeling staff flows. We therefore decided to develop our own dynamic workforce optimization model.
In this paper we will define how we distinguish three types of staff flows in The Business Simulator: inflow, throughput and output. Once these types are determined, we will elaborate more on how these can be modeled and what objective function will optimize a desired future workforce.
Mathematical models in a Human Resource Context
The simplest form of a workforce modeling system treats the modeling of a group of people having the same job. The size of the group changes due to recruitment and outflow. More complex systems incorporate a set of different function levels and enable the modeling of a flow of promotions.
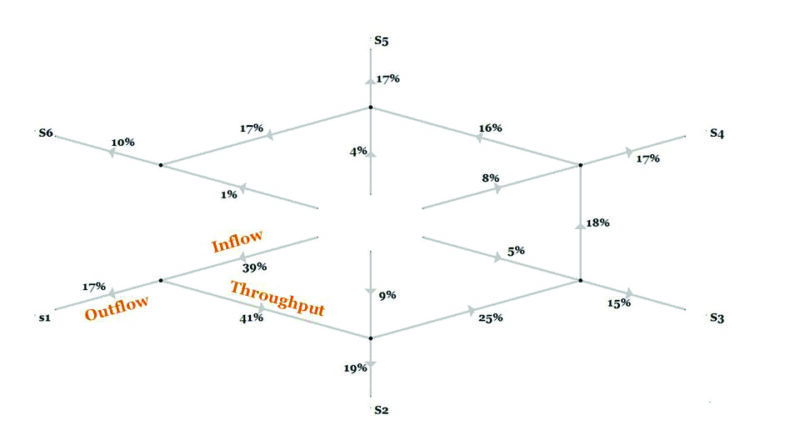
In this article we will incorporate the workforce flows for a company having six different function levels and recruiting mainly people from university. This can be seen as a common and general business model for amongst others banks, insurance companies, governmental organizations and hospitals. The generic function levels are named: S1 up to S6. As modeling environment we decided to use AIMMS, since this is a very powerful language in visualizing data flows in networks while it is a broadly recognized optimization package as well.
Figure 1 shows the flows of a workforce having the six function levels, for a given year. It is created as a circular network graph, using nodes and arcs to visualize the flows from and to function levels. The black nodes are defined as the function levels. In addition, the displayed percentages show the proportion of inflow, throughput (promotion) and outflow.
In- and outflow probabilities can easily be defined by taking the proportion of in- and outflow of total employers. The promotion scheme is usually presented by a throughput matrix. Several historical career paths and the capability framework in the career model were studied in obtaining realistic throughput probability values.
Desirable Workforce Composition
Besides the historical workforce flows, we need to specify suitable ratios per function level to build effective teams. By using these ratios we can fill in the seniority degree of freedom, i.e., we can determine the appropriate seniority level of new joiners. Another way of looking at these desirable staff ratios is viewing these as a desirable population pyramid for the staff.
We will elaborate on the other input variables for The Business Simulator after we have explained how the optimization engine of this model works.
From the Mehlmann model to The Business Simulator
To give a flavor of what these models from the literature look like, we describe a representative model designed by Mehlmann. It uses dynamic programming – in which every decision influences future decisions – to determine optimal promotion schemes and recruiting targets (Mehlmann, 1980). The set of decision problems consists of deciding on promotions and inflow every year, such that the deviation from a desirable workforce structure is as small as possible.
Although the Mehlmann model offers good insight in the principles of manpower planning models, we cannot use this model for our purposes due to two reasons. First of all, the model only focuses on the structure of resource pools and does not take into account the available staffing budget. Secondly, the model needs the future total sizes of resource pools as input parameters, whereas we would like our model to consider these as output parameters.
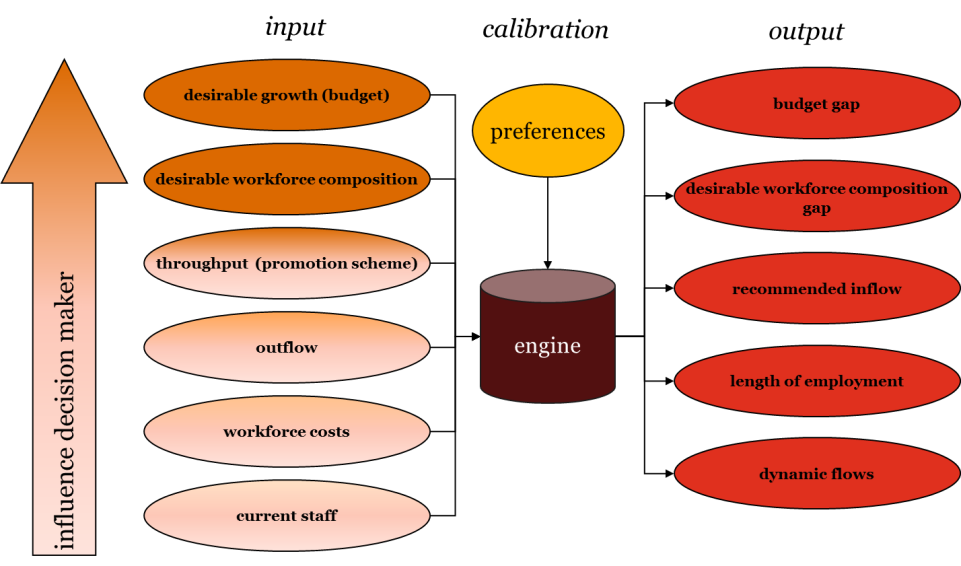
The first conclusion from studying the Mehlmann model is that we can keep the model quite simple by treating the promotion scheme as a fixed input parameter (rather than decision variables), and the inflow at different function levels as the only decision variable. Furthermore, a shift in emphasis is necessary to fit the particular model needs. Unlike Mehlmann, we also want to exploit predictions about future staffing costs. Therefore we combined those basic principles into a new PwC model: The Business Simulator. Our model is summarized in Figure 2.
On the left we have all input parameters. We listed these parameters in decreasing order of influence the decision maker (i.e., the HR manager) has to determine them. The current staff is given and an organization hardly has influence on the costs of the workforce. Outflow and promotions start to become easier to influence and the organization at stake is totally free to choose the desirable workforce composition and to predict what future budget they will spend on their workforce.
Before we run the model to compute outputs, we can set our preferences. Regarding these preferences, one can think of the calibration method or the number of years to predict. The most important outputs are the budget gap, the desirable workforce composition gap and the recommended inflow. The first is the difference between the future budget and the amount computed by the model to spend by the organization on their workforce. The second gap is the deviation per function level between the desired number of FTE and the actual number computed by the model. Having the outflow and the throughput per function level, the model determines the recommended inflow per year and per function level. Based on this output the organization can build its recruitment strategy.
Next to these three outputs, we also want to track the resulting average length of employment. This can support in the quantification of social plans, in which the length of employment is an important factor to decide whether or not an employee can stay. Finally, we want to be able to follow the dynamics of various flows of resources. —›
Creating Impact in a Boardroom Setting
In our opinion one of the essential characteristics of any type of model is the capability to be suited to many different circumstances, which cannot be predicted precisely beforehand. Examples are the introduction of new function levels and unemployment. As people started to build tools that could help to define actions in such occasions, two classes of models started to evolve: explanatory models and normative models.
Explanatory models are limited to yield insight in how the current workforce policy works and how it would react to certain stimuli. These models range from very simple models that can be used by almost any type of organization, to very elaborate complex stochastic simulation models for the study of specific types of HR flows.
Normative models – sometimes also called binding models – are more powerful in the sense that they can compute a set of optimal decisions, given a set of objectives and predictions about changing circumstances. The set of objectives is normally translated into one value by using an object function. Within the set of normative models, a distinction can be made between models that make use of object functions with or without targets. Without targets, the normative model would for example compute a set of decisions that maximize profit, or minimize outflow. An example of a normative model with a target is the attempt to arrive at a pre-set leverage of senior employees.
One important thing to realize as a model developer is not to forget the ultimate goal of the model. In case of The Business Simulator the final model will be used to support HR managers and directors making more solid policy by showing the quantified impact of their decisions. This implies the model builder should also spend enough time in the design of the output and, more common, on the user-friendliness. Of course, the algorithm should be right as well, but that is the basic expertise and knowledge you might expect from an analytical consultant.
In conclusion, we see building quantitative models as an iterative process in which the client is strongly involved. The model should be able to anticipate quickly on questions uprising in demo presentations. Consequently, the modeler needs to have a grasp of storytelling: “A new kind of professional has emerged, the data scientist, who combines the skills of software programmer, statistician and storyteller/artist to extract the nuggets of gold hidden under mountains of data” (The Economist, 2010). •
References
Mehlmann, A. (November, 1980). “An Approach to Optimal Recruitment and Transition Strategies for Manpower Systems using Dynamic Programming.” The Journal of the Operational Research Society, Vol. 31, No. 11, pp.1009-1015
Cukier, K. (February, 2010). “Data, data everywhere”, The Economist
Text by: Jacques de Swart, Lau Akkermans and Linda Vos