Unilateral support equilibria

July 2, 2020March 1, 2021 Nekst-Online 220 Views

The concept of Nash equilibria is the most well-known concept within non-cooperative game theory and is widely used in many other fields. In a Nash equilibrium, every player maximizes his or her own pay-off with respect to the Nash equilibrium strategy combination of the other players. On the other hand, in a Berge equilibrium, every player’s pay-off is maximized by the group of all other players and this player is thus supported by them. We introduce a new equilibrium concept based on individual support rather than the group support underlying a Berge equilibirum. In a unilateral support equilibrium, every player is supported by every other player individually. Written by: Job Schouten

Introduction

Non-cooperative game theory deals with situations of interaction and conflict between individuals (or players). Within the field of non-cooperative game theory, special attention goes to providing equilibrium concepts to somehow solve these con- flicts. Such a concept should answer the question how to determine a good strategy if you do not know the strategies of the other players beforehand.

The standard Nash equilibrium concept is defined by Nash (1951, [5]) and is based on the fact that no player should have an incentive to unilaterally deviate from an equilibrium strategy.

The idea of Berge (1957, [1]) yields an equilibrium concept in which players are not maximizing their own pay-offs, but maximize the other players’ pay-off instead. This follows the motto of The Three Musketeers: ‘one for all, and all for one’: every player supports (as part of a larger group) every other player and all other players support every single player.

However, the support relation in a Berge equilibrium is re- stricted to group support as the group of all players except for one single player supports the single player in the best way possible. To do so, they have to coordinate their actions, which can cause coordination issues for the players. To avoid these rather complex coordination issues, we consider individ- ual support rather than group support.

Our main idea¹is to introduce a new equilibrium concept,

which is based on support relations between the individual players. We model these support relations by bijections and in particular, by using derangements, in which there are no fixed points. The interpretation of such a derangement is that every player supports exactly one other player and every player is supported by exactly one other player. Then, a uni- lateral support equilibrium is a strategy combination that is unilaterally supportive with respect to every possible derange- ment.

Preliminaries

First, we provide the preliminaries on non-cooperative game theory and the two equilibrium concepts. A non-cooperative (strategic) game is a triple

$G = (N,(X_i)_{i \in N},(\pi_i)_{i \in N}),$

where N is a non-empty, finite set of players, with $|N| \geq 2$ , $X_i$ the set of strategies for player $i \in N$ and $\pi_i : x \rightarrow \R$ the pay-off function of player i ∈ N. Here, $X = \prod_{i \in N} X_i$ is called the set of strategy combinations.

A strategy combination $x^* \in X$ is called a Nash equilibrium if for every i ∈ N it holds that

$\pi_i(x^*_{-i},x_i) \leq \pi_i(x^*_{-i},x^*_i),$

for every $x_i \in X_i$ (Nash, 1950, [4]) $.^2$ The set of Nash equilibria for G is denoted by $NE(G)$ . For $i \in N$ and $x_{-i} \in X_{-i},$ define the set of best reply strategies against $x_{-i}$ , $BR_i(x_{-i}),$ as follows:

$BR_i(x_{-i}) = \{ x_i \in X_i | \pi_i(x_{-i},x^{'}_i) \leq \pi_i(x_{-i},x_i) \hspace{5mm} \forall x^{'}_i \in X_i \}.$

Clearly, $x^* \in NE(G)$ if and only if $x_i^* \in BR_i(x^*_{-i})$ for every $i \in N$ .

A strategy combination $x^* \in X$ is called a Berge equilibrium if for every $i \in N$ it holds that

$\pi_i(x^*_i,x_{-i} \leq \pi_i(x_i^*,x_{-i}^* ),$

for every $x_{-i} \in X_{-i}$ (Berge, 1957, [1]). The set of Berge equilibria for G is denoted by $BE(<em>G</em>)$ . For $i \in N$ and $x_i \in X_i$ define the set of best support strategy combinations against $x_i$ , $BS_i(x_i)$ , as follows (cf. Musy et al., 202, [3]):

$BS_i(x_i) = \{x_{-i} \in X_{-i} | \pi_i(x_i,x^{'}_{-i} \leq \pi_i(x_i,x_{-i}) \hspace{5mm} \forall x^{'}_{-i} \in X_{-i}$

Clearly, $x^{*} \in BE(G)$ if and only if $x^{*}_{-i} \in BS_i(x_i^*) \hspace{5mm} \forall i \in N$ .

Set $N = \{ 1,2,...,n \}$ . A bijection $\sigma : N \rightarrow N$ is a map that is both surjective (onto) and injective (one-to-one) and is denoted by $\sigma = (\sigma (1),\sigma (2),...,\sigma (n))$ . The set of all such bijections is denoted by $\Pi (N)$ . The identity bijection is denoted by Id, i.e. $Id = (1,2,...,n)$ . In the context of supportive behavior, a bijection $\sigma \in \Pi (N)$ should be interpreted as follows: player $i \in N$ supports player $\sigma (i) \in N$ . Finally, we introduce the set of all derangements, given by

$D(N) = \{ \delta \in \Pi (N) | \delta (i) = i \hspace{5mm} i \in N \}.$

Unilateral support equilibria

We start by introducing unilaterally supportive strategy com- binations with respect to a bijection. Afterwards, this is gen- eralized to the definition of a unilateral support equilibrium, where the dependence on a certain bijection is removed.

Definition 1 Let G be a non-cooperative game and let $\sigma \in \Pi (N)$ be a bijection. A strategy combination $x^* \in X$ is called unilaterally supportive with respect to $\sigma$ if, for every $i \in N$ ,

$\pi_{\sigma (i)} (x^*_{-i},x_i) \leq \pi_{\sigma (i)} (x_{-i}^*,x_i^*),$

for every $x_i \in X_i$ . The set of such strategy combinations isdenoted by $USE_{\sigma}(G)$ ⊲ .

In a unilaterally supportive strategy combination with respect to a bijection $\sigma$ , player $i \in N$ supports player $\sigma (i) \in N$ in the best way possible. This means that player i is going to maximize the pay-off of player $\sigma (i)$ , given the unilaterally supportive strategy combination of the other players. This implies that every set of unilaterally supportive strategy combinations with respect to a bijection $\sigma$ of a game G coincides with the set of Nash equilibria of the game $G_{\sigma}$ with twisted pay-off functions, in which player $i$ ‘s pay-off function is replaced by the pay-off function of player $\sigma(i)$ , i.e.,

$G_{\sigma} = \large{(} N, (X_i)_{i \in N},(\pi_{\sigma (i)})_{i \in N} \large{)}$

Proposition 1 Let G be a non-cooperative game and let $\sigma \in \Pi (N)$ be a bijection. Then it holds that

$USE_{\sigma}(G) = NE(G_{\sigma}).$

Remark Note that if one applies Proposition 1 to the iden- tity bijection, it follows that $USE_{Id}(G) = NE(G)$ . For every bijection, the corresponding set of unilaterally sup- portive strategy combination with respect to that bijection can be defined. However, only derangements really reflect the idea of supportive behavior. If a player is mapped to himself, then this player does not support another player. The set of unilaterally supportive strategy combinations with respect to a derangement has the disadvantage that it is not anonymous in the sense that it relies on the predetermined support rela- tions given by the derangement. For this reason, in order to define the set of unilateral support equilibria, we will consider the set of unilaterally supportive strategy combinations with respect to all derangements.

Definition 2 Let G be a non-cooperative game. Then the set of unilateral support equilibria is defined as

$USE(G) = \bigcap\limits_{\delta \in D(N)} USE_{\delta}(G). \hspace{5mm} ⊲$

The following theorem provides an alternative formulation of the set of unilateral support equilibria in terms of the pay-off functions. This contrasts the definition, which is formulated as the intersection of sets of unilaterally supportive strategy

combinations. The theorem clearly highlights the underlying feature of unilaterally supportive behavior.

Theorem 1 Let G be a non-cooperative game and let $x^* \in X$ be a strategy combination. Then $x^* \in USE(G)$ if and only if for every $i \in N$ and every $j \in N \backslash \{ i \}$ it holds that

$\pi_i(x^*_{-j},x_j) \leq \pi_i(x_{-j}^*,x_j^*) \hspace{5mm} \forall x_j \in X_j$

Unilateral support, Berge and Nash equilibria

Theorem 1 shows that in a unilateral support equilibrium, ev- ery player is supported by every other player individually. In a Berge equilibrium, every player is supported by the group of all other players together. Subsequently, every Berge equilibrium is in fact a unilateral support equilibrium. This result is based on the fact that a Berge equilibrium is unilaterally supportive with respect to any derangement.

Theorem 2 Let G be a non-cooperative game. Then it holds that $BE(G) \subseteq USE(G)$ .

For a two-person game, however, the group of all other players together consists of only one other player. This implies that the set of Berge equilibria consists of those strategy combi- nations in which every player is supported by the other player in the best way possible. Hence, the set of Berge equilibria coincides with the set of unilateral support equilibria.

Proposition 2 Let G be a non-cooperative game with |N| = 2. Then it holds that

$BE(G) = USE(G) = NE(G_{(2,1)}).$

To conclude, we give an example of a game in which there is a unilateral support equilibrium, while there is no Berge equilibrium. This shows that the inclusion of Theorem 2 is a strict inclusion.

Here, $G$ is represented as a trimatrix game $.^3$

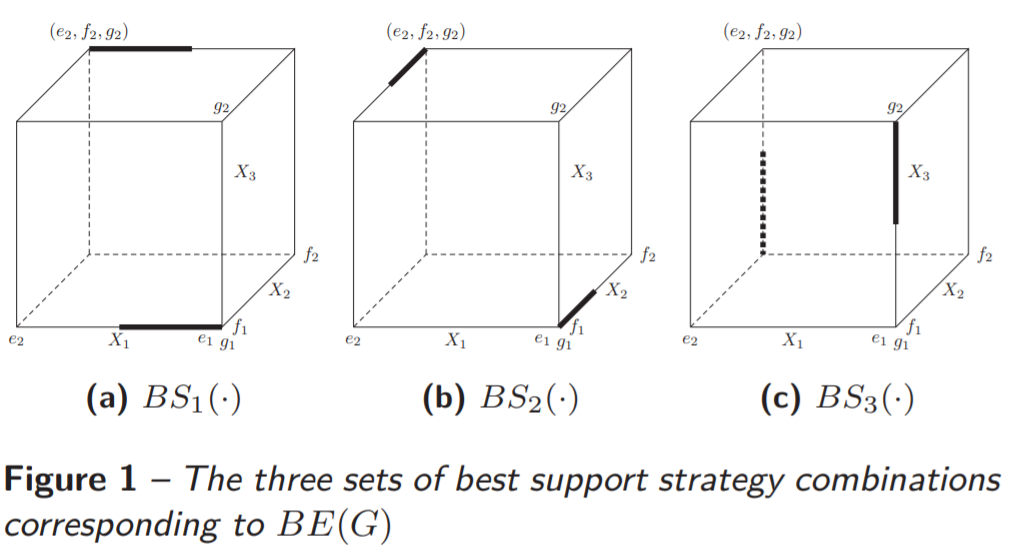
First, we show that there are no Berge equilibria by using the sets of best support strategy combinations, which are presented in Figure 1. For example, Figure 1a shows that, if player 1 chooses a $\lambda e_1 + (1 - \lambda) e_2 \in X_1$ with $\lambda \in [\frac{1}{2},1]$ (bottom part), then the best thing players 2 and 3 together can do to support player 1 is the strategy combination $(f_1,g_1) \in X_{-1}$ .

Using Figure 1, it can be readily seen that the intersection between the three sets of best support strategy combinations is empty. Hence, $BE(G) = \emptyset$ .

Secondly, we show that $(e_1,f_1,g_1) \in USE(G)$ . Using the characterization provided in Theorem 1, this can be seen from the following six inequalities:

$\pi_1 (e_1,x_2,g_1) \leq 1 = \pi_1 (e_1, f_1, g_1) \hspace{5mm} x_2 \in X_2;$

$\pi_1 (e_1,f_1,x_3) \leq 1 = \pi_1 (e_1, f_1, g_1) \hspace{5mm} x_3 \in X_3;$

$\pi_2 (x_1,f_1,g_1) \leq 1 = \pi_2 (e_1, f_1, g_1) \hspace{5mm} x_1 \in X_1;$

$\pi_2 (e_1,f_1,x_3) \leq 1 = \pi_2 (e_1, f_1, g_1) \hspace{5mm} x_3 \in X_3;$

$\pi_3 (x_1,f_1,g_1) \leq 0 = \pi_3 (e_1, f_1, g_1) \hspace{5mm} x_1 \in X_1;$

$\pi_3 (e_1,x_2,g_1) \leq 0 = \pi_3 (e_1, f_1, g_1) \hspace{5mm} x_2 \in X_2;$

Consequently, $USE(G) = \emptyset$ .

Finally, note that also $NE(G) = \emptyset$ , since $(e_1, f_1, g_2) \in NE(G).$ △

_______________________

1) This Triangle is a short version of our paper ‘Unilateral support equilibria’, Schouten, Borm, Hendrickx (2019), [6].

2) Note that $x_{-i} = (x_j)_{j \in N \backslash \{ i \} } \in X_{-i} = \prod_{ j \in N \backslash \{ i \} } X_j$ in general.

3) That is, in short, player 1 randomizes over $e_1$ and $e_2$ , player 2 over $f_1$ and $f_2$ and player 3 over $g_1$ and $g_2$ . The pay-off functions are the expected pay-offs.

References

[1] Berge, C. (1957). Théorie générale des jeux à n personnes. Gauthier-Villars, Paris.

[2] Corley, H. (2015). A mixed cooperative dual to the Nash equilibrium. Game Theory, 2015, article ID 647246.

[3] Musy, O., A. Pottier, and T. Tazdaït (2012). A new theorem to find Berge equilibria. International Game Theory Review, 14, article ID 1250005.

[4] Nash, J. (1950). Equilibrium points in n-person games. Pro- ceedings of the National Academy of Sciences of the USA, 36, 48–49

[5] Nash, J. (1951). Non-cooperative games. Annals of Mathematics, 54, 286–295.

[6] Schouten, J., P. Borm and R. Hendrickx (2019). Unilateral support equilibria. Journal of Mathematical Psychology, 93, 102295.

You May Also Like

Over-The-Counter Trades in Longevity Risk

Estimation of Time Varying Partial Correlation Networks

What Is the Pooling Problem?