The Individual Settlement Allocation Procedure
A mutual liability problem comprises a network of interacting economic agents. Consequently, these agents have mutual liabilities as well as assets to be used for monetary transactions. If all agents want to settle their claims, the question at hand is how to allocate the total assets among them. To this end, agents can use the Individual Settlement Allocation Procedure, where agents act on their own and yet reach a consensus on the allocation.
Written by: Martijn Keetelaars
Mutual liability problems
The notion of a mutual liability problem is perhaps best explained by means of an example with three agents. For the sake of expositional convenience, these agents are Alice, Bob and Charlie, i.e. ![]() . Alice, Bob and Charlie are mutually indebted, which can be represented by a claims matrix
. Alice, Bob and Charlie are mutually indebted, which can be represented by a claims matrix ![]() , where element
, where element ![]() indicates the claim of agent
indicates the claim of agent ![]() on agent
on agent ![]() . With regard to this example,
. With regard to this example,
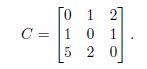
For instance, Alice owes 1 to Bob and 2 to Charlie, however Alice has a claim of 1 on Bob and a claim of 5 on Charlie. In addition to this, each of them owns assets, which are represented by an estate vector ![]() , where element
, where element ![]() indicates the estate belonging to agent
indicates the estate belonging to agent ![]() . Alice has an estate of 2, whereas both Bob and Charlie have an estate of 1. That is,
. Alice has an estate of 2, whereas both Bob and Charlie have an estate of 1. That is, ![]() .
.
Suppose that Alice is running short of money and thus asks Bob and Charlie to pay off their respective debts of one and five euros to her. Even though Bob is able to do so, Charlie can only pay her at most one euro. Therefore, he turns to Alice and Bob and demands that they pay him back. Alice can pay off her debt of two euros to Charlie, but Bob does not have enough and consequently asks Alice and Charlie to pay him. Alice pays Bob one euro which Bob uses to pay Charlie. At this point both Alice and Bob are debt-free and Charlie owns 4, i.e. ![]() . Unfortunately, this is still insufficient for Charlie to pay off his debts. Therefore the assets in this network are insufficient for all claims to be settled. This gives rise to the following question: how should the total available amount of assets in this network be allocated among the agents, while taking the mutual liabilities of all agents into account?
. Unfortunately, this is still insufficient for Charlie to pay off his debts. Therefore the assets in this network are insufficient for all claims to be settled. This gives rise to the following question: how should the total available amount of assets in this network be allocated among the agents, while taking the mutual liabilities of all agents into account?
On solving mutual liability problems
If you are familiar with bankruptcy problems, you might have noticed that mutual liability problems are a generalization of such problems. In a bankruptcy problem there is a single non-negative estate, ![]() , that has to be allocated among a finite set of claimants,
, that has to be allocated among a finite set of claimants, ![]() , where each claimant
, where each claimant ![]() has a non-negative claim,
has a non-negative claim, ![]() , on the estate. In order to determine an allocation of the estate, one can make use of so-called bankruptcy rules. Such rules prescribe for each bankruptcy problem how to allocate the estate among the claimants. To put it mathematically, let
, on the estate. In order to determine an allocation of the estate, one can make use of so-called bankruptcy rules. Such rules prescribe for each bankruptcy problem how to allocate the estate among the claimants. To put it mathematically, let ![]() denote the set of all bankruptcy problems
denote the set of all bankruptcy problems ![]() on
on ![]() , where
, where ![]() denotes a finite set of agents. A bankruptcy rule
denotes a finite set of agents. A bankruptcy rule ![]() assigns to each bankruptcy problem
assigns to each bankruptcy problem ![]() a non-negative allocation
a non-negative allocation ![]() such that
such that
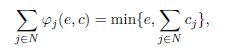
and ![]() for all
for all ![]() .
.
Groote Schaarsberg, Reijnierse and Borm (2018) present a method of solving mutual liability problems that makes use of a so-called payment matrix, which is a non-negative matrix ![]() where element
where element ![]() indicates the payment of agent
indicates the payment of agent ![]() to agent
to agent ![]() . These payments are derived through bankruptcy rule
. These payments are derived through bankruptcy rule ![]() . A formal definition of
. A formal definition of ![]() -transfer schemes is given below.
-transfer schemes is given below.
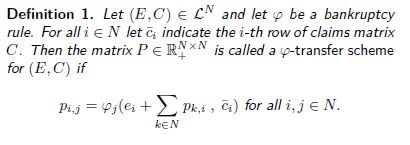
Thus, the amount agent ![]() has to pay to agent
has to pay to agent ![]() is determined by the solution of the bankruptcy problem agent
is determined by the solution of the bankruptcy problem agent ![]() faces with estate equal to the current estate of agent
faces with estate equal to the current estate of agent ![]() plus what agent
plus what agent ![]() receives from other agents, and with claims equal to the claims on the estate of agent
receives from other agents, and with claims equal to the claims on the estate of agent ![]() .
.
The set of all possible ![]() -transfer schemes for
-transfer schemes for ![]() is denoted by
is denoted by ![]() .
.
Groote Schaarsberg et al. (2018) show that there always exists at least one ![]() -transfer scheme. Therefore, on the basis of these payments
-transfer scheme. Therefore, on the basis of these payments ![]() they define the
they define the ![]() -transfer allocation
-transfer allocation ![]() . That is, for
. That is, for ![]() the allocation is equal to
the allocation is equal to
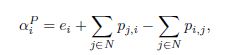
so the allocation to agent ![]() equals the estate plus the net payments of agent
equals the estate plus the net payments of agent ![]() . Interestingly, Groote Schaarsberg et al. (2018) show that for
. Interestingly, Groote Schaarsberg et al. (2018) show that for ![]() it holds that
it holds that ![]() . Hence, all
. Hence, all ![]() -transfer schemes that correspond with a mutual liability problem give the same allocation.
-transfer schemes that correspond with a mutual liability problem give the same allocation.
Nevertheless, a drawback of working with ![]() -transfer schemes is that solving it by hand can be quite complicated even for problems with three agents. This is due to the fact that a system of dependent equations has to be solved; and in order to do so, one often needs to exploit characteristics of the problem and properties of the bankruptcy rule
-transfer schemes is that solving it by hand can be quite complicated even for problems with three agents. This is due to the fact that a system of dependent equations has to be solved; and in order to do so, one often needs to exploit characteristics of the problem and properties of the bankruptcy rule ![]() . In the situation of Alice, Bob and Charlie as discussed in the previous section, the following set of equations has to be solved:
. In the situation of Alice, Bob and Charlie as discussed in the previous section, the following set of equations has to be solved:
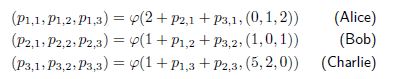
In addition to this, Groote Schaarsberg et al. (2018) make quite a restrictive assumption. They assume that an independent autohority is assigned the task to allocate the total estate among the agents. This assumption can cause their solution method to fall apart. For instance, if Alice does not want to disclose her debts, then there will be no consensus about the allocation. Alice’s privacy is more important to her. In spite of this, agents can take matters into their own hands instead and still reach a consensus on how to allocate the total estate among them.
Individual Settlement Allocation Procedure
The Individual Settlement Allocation Procedure is a recursive procedure put forth as a solution to the complications the ![]() -transfer scheme approach brings about. This procedure states that agents settle their claims individually which ultimately leads to a unique allocation. More specifically, in each step each agent uses the same bankruptcy rule to allocate his estate among the others. Therefore agents make payments to each other, which implies that the total estate is reallocated. In addition to that, these payments lower the mutual liabilities. The result is a new mutual liability problem to which the same procedure can be applied. This process can either go on indefinitely or terminate at a point where no agent makes any further payments. However, even if payments go on indefinitely, it can be shown that the sequence of estate vectors that is generated by the Individual Settlement Allocation Procedure has a finite limit. Hence, there always exists a unique allocation.
-transfer scheme approach brings about. This procedure states that agents settle their claims individually which ultimately leads to a unique allocation. More specifically, in each step each agent uses the same bankruptcy rule to allocate his estate among the others. Therefore agents make payments to each other, which implies that the total estate is reallocated. In addition to that, these payments lower the mutual liabilities. The result is a new mutual liability problem to which the same procedure can be applied. This process can either go on indefinitely or terminate at a point where no agent makes any further payments. However, even if payments go on indefinitely, it can be shown that the sequence of estate vectors that is generated by the Individual Settlement Allocation Procedure has a finite limit. Hence, there always exists a unique allocation.
In order to illustrate this procedure, suppose that Alice, Bob and Charlie apply the proportional rule PROP. This rule divides the estate among the claimants proportional to the claims and is defined by

Otherwise, ![]() for all
for all ![]() . Hence, in the first step
. Hence, in the first step
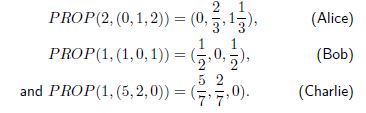
For instance, this means that Alice pays ![]() to Bob and
to Bob and ![]() to Charlie. Subsequently, reallocate the total estate and reduce the mutual claims by the payments:
to Charlie. Subsequently, reallocate the total estate and reduce the mutual claims by the payments:
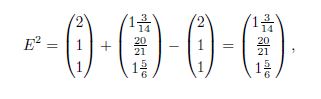
and
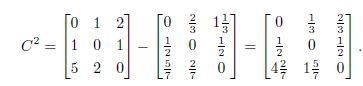
Therefore, in the second step Alice has sufficient funds to fully pay her remaining debts. On the other hand, Bob and Charlie do not. Thus,
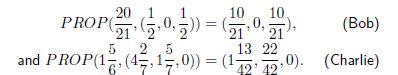
Again, reallocate the total estate and reduce mutual claims to get
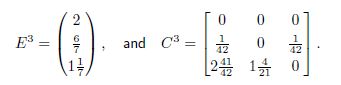
At this moment, Bob can pay off his remaining debts while Charlie still cannot. Charlie first allocates ![]() by giving
by giving ![]() to Alice and
to Alice and ![]() to Bob. Finally, Charlie will only receive one more payment of
to Bob. Finally, Charlie will only receive one more payment of ![]() from Bob which he will allocate among Alice and Bob. Bob’s payment is still not sufficient, so ultimately Charlie goes bankrupt. Therefore, the limit of the sequence of estate vectors is attained in a finite number of steps and can shown to be equal to
from Bob which he will allocate among Alice and Bob. Bob’s payment is still not sufficient, so ultimately Charlie goes bankrupt. Therefore, the limit of the sequence of estate vectors is attained in a finite number of steps and can shown to be equal to ![]() . Thus, the Individual Settlement Allocation Procedure prescribes that in this case Alice receives
. Thus, the Individual Settlement Allocation Procedure prescribes that in this case Alice receives ![]() , Bob receives
, Bob receives ![]() , and Charlie receives
, and Charlie receives ![]() .
.
Unlike the previous example, payments can also go on indefinitely such as in the following mutual liability problem:
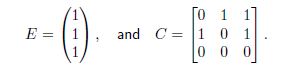
Suppose all agents apply the proportional rule. The proportional rule prescribes that in each step agents 1 and 2 allocate their estate equally among their claimants, while both only receive half of that amount back. Moreover, agent 3 does not make any payments at all.
Therefore, agents 1 and 2 ultimately pay
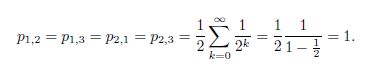
Thus, the allocation is equal to
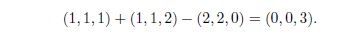
An interesting relationship
In contrast to the ![]() -transfer scheme approach of Groote Schaarsberg et al. (2018), the Individual Settlement Allocation Procedure partitions the original bankruptcy problem each agent faces into a — possibly infinite — series of sub-problems that are solved separately. There is a particular property of bankruptcy rules that allows you to partition a bankruptcy problem without changing the allocation. This is the composition up property defined below.
-transfer scheme approach of Groote Schaarsberg et al. (2018), the Individual Settlement Allocation Procedure partitions the original bankruptcy problem each agent faces into a — possibly infinite — series of sub-problems that are solved separately. There is a particular property of bankruptcy rules that allows you to partition a bankruptcy problem without changing the allocation. This is the composition up property defined below.
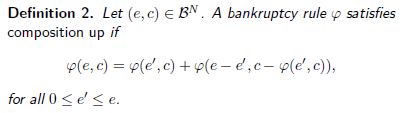
One can show that for the class of bankruptcy rules that satisfy the composition up property, the resulting allocations of both discussed solution methods coincide. In other words, agents are not obliged to disclose their debts in case such bankruptcy rules are applied. As a matter of fact, one can show that the proportional rule satisfies composition up. Therefore, for any mutual liability problem ![]() it holds that
it holds that
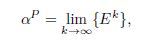
where ![]() and
and ![]() is the sequence of estate vectors generated by the Individual Settlement Allocation Procedure in which agents apply the proportional rule.
is the sequence of estate vectors generated by the Individual Settlement Allocation Procedure in which agents apply the proportional rule.
References
[1] Groote Schaarsberg, M., Reijnierse, H. and Borm, P. (2018).
On Solving Mutual Liability Problems. Mathematical Methods of Operations Research, 87, 383-409.




